题目内容
【题目】若不等式a|x|>x2﹣ ![]() 对任意x∈[﹣1,1]都成立,则实数a的取值范围是( )
对任意x∈[﹣1,1]都成立,则实数a的取值范围是( )
A.( ![]() ,1)∪(1,+∞)
,1)∪(1,+∞)
B.(0, ![]() )∪(1,+∞)??
)∪(1,+∞)??
C.( ![]() ,1)∪(1,2)
,1)∪(1,2)
D.(0, ![]() )∪(1,2)
)∪(1,2)
【答案】A
【解析】解:设f(x)=a|x| , g(x)=x2﹣ ![]() ,
,
当x∈[﹣1,1]时,g(x)∈[﹣ ![]() ,
, ![]() ],
],
∵f(x)和g(x)都是偶函数,
∴只要保证当x∈[0,1]时,不等式a|x|>x2﹣ ![]() 恒成立即可.
恒成立即可.
当x∈[0,1]时,f(x)=ax ,
若a>1时,f(x)=ax≥1,此时不等式a|x|>x2﹣ ![]() 恒成立,满足条件.
恒成立,满足条件.
若0<a<1时,f(x)=ax为减函数,而g(x)为增函数,
此时要使不等式a|x|>x2﹣ ![]() 恒成立,则只需要f(1)>g(1)即可,
恒成立,则只需要f(1)>g(1)即可,
即a>1﹣ ![]() =
= ![]() ,
,
此时 ![]() <a<1,
<a<1,
综上 ![]() <a<1或a>1,
<a<1或a>1,
故选:A.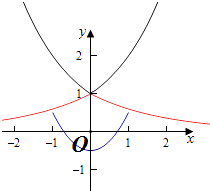

练习册系列答案
相关题目