ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ÷÷Ή”ΖΔ―Ω¬ ”κ÷γ“ΙΈ¬≤ν”–ΙΊ.Ρ≥―–ΨΩ–‘―ßœΑ–ΓΉιΕ‘¥ΥΫχ––―–ΨΩΘ§ΥϊΟ«Ζ÷±πΦ«¬ΦΝΥ3‘¬12»’÷Ν3‘¬16»’ΒΡ÷γ“ΙΈ¬≤ν”κΟΩΧλ100Ω≈Ρ≥÷÷÷÷Ή”Ϋΰ≈ίΚσΒΡΖΔ―Ω ΐΘ§»γœ¬±μΘΚ

Θ®IΘ©¥”3‘¬12»’÷Ν3‘¬16»’÷–»Έ―Γ2ΧλΘ§Φ«ΖΔ―ΩΒΡ÷÷Ή” ΐΖ÷±πΈΣcΘ§dΘ§«σ ¬ΦΰΓΑc,dΨυ≤Μ–Γ”Ύ25Γ±ΒΡΗ≈¬ ΘΜ
Θ®IIΘ©«κΗυΨί3‘¬13»’÷Ν3‘¬15»’ΒΡ»ΐΉι ΐΨίΘ§«σ≥ωyΙΊ”ΎxΒΡœΏ–‘ΜΊΙιΖΫ≥Χ![]() ΘΜ
ΘΜ
Θ®IIIΘ©»τ”…œΏ–‘ΜΊΙιΖΫ≥ΧΒΟΒΫΒΡΙάΦΤ ΐΨί”κ ΒΦ ΐΨίΈσ≤νΨυ≤Μ≥§Ιΐ2Ω≈Θ§‘ρ»œΈΣΜΊΙιΖΫ≥Χ «Ω…ΩΩΒΡΘ§ ‘”Ο3‘¬12»’”κ16»’ΒΡΝΫΉι ΐΨίΦλ―ιΘ§Θ®IIΘ©÷–ΒΡΜΊΙιΖΫ≥Χ «ΖώΩ…ΩΩΘΩ
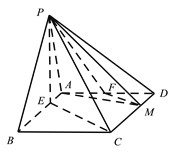
ΓΨ¥πΑΗΓΩ(1) ![]() ;(2)
;(2) ![]() ;(3)œξΦϊΫβΈω.
;(3)œξΦϊΫβΈω.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷Έω:(1)”…Ν–ΨΌΖ®ΒΟ≥ω¥”5Χλ÷–»Έ―Γ2ΧλΒΡΜυ±Ψ ¬Φΰ, ―Γ≥ωΒΡΕΰΧλ÷÷Ή”ΖΔ―Ω ΐΨυ≤Μ–Γ”Ύ25ΒΡΜυ±Ψ ¬Φΰ,ΗυΨίΙ≈ΒδΗ≈–ΆΒΟ≥ωΗ≈¬ ;(2)œ»«σ≥ωΤΫΨυ ΐΚΆ![]() ¥ζ»κΙΪ Ϋ,«σ≥ωœΏ–‘ΜΊΙιΖΫ≥Χ;(3)ΫΪ
¥ζ»κΙΪ Ϋ,«σ≥ωœΏ–‘ΜΊΙιΖΫ≥Χ;(3)ΫΪ![]() ΚΆ
ΚΆ![]() ¥ζ»κΖΫ≥Χ,”κΘ®IIΘ©÷–ΒΡΜΊΙιΖΫ≥ΧΫχ––±»Ϋœ,ΒΟ≥ωΫα¬έ.
¥ζ»κΖΫ≥Χ,”κΘ®IIΘ©÷–ΒΡΜΊΙιΖΫ≥ΧΫχ––±»Ϋœ,ΒΟ≥ωΫα¬έ.
‘ΧβΫβΈω:Θ®ΔώΘ©¥”5Χλ÷–»Έ―Γ2ΧλΘ§Ι≤”–10ΗωΜυ±Ψ ¬ΦΰΘΚΘ®12»’Θ§13»’Θ©Θ§Θ®12»’Θ§14»’Θ©Θ§Θ®12»’Θ§15»’Θ©Θ§
Θ®12»’Θ§16»’Θ©Θ§Θ®13»’Θ§14»’Θ©Θ§Θ®13»’Θ§15»’Θ©Θ§Θ®13»’Θ§16»’Θ©Θ§Θ®14»’Θ§15»’Θ©Θ§Θ®14»’Θ§16»’Θ©Θ§Θ®15»’Θ§16»’Θ©Θ°
―Γ≥ωΒΡΕΰΧλ÷÷Ή”ΖΔ―Ω ΐΨυ≤Μ–Γ”Ύ25Ι≤”–3ΗωΜυ±Ψ ¬ΦΰΘΚΘ®13»’Θ§14»’Θ©Θ§Θ®13»’Θ§15»’Θ©Θ§Θ®14»’Θ§15»’Θ©Θ°
Γύ ¬ΦΰΓΑ![]() Ψυ≤Μ–Γ”Ύ25Γ±ΒΡΗ≈¬ ΈΣ
Ψυ≤Μ–Γ”Ύ25Γ±ΒΡΗ≈¬ ΈΣ![]() .
.
Θ®ΔρΘ©![]() Θ°
Θ° ![]() 5Θ°
5Θ° ![]() =2Θ°
=2Θ°
Γύ![]() .
.
Γύ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΈΣ
ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΈΣ![]() .
.
Θ®ΔσΘ©Β±![]() ±Θ§
±Θ§ ![]() Θ°
Θ°
Β±![]() ±Θ§
±Θ§ ![]() Θ°
Θ°
ΓύΜΊΙιΖΫ≥Χ![]() «Ω…ΩΩΒΡΘ°
«Ω…ΩΩΒΡΘ°
ΒψΨΠ:ΨΏ”–“‘œ¬ΝΫΗωΧΊΒψΒΡΗ≈¬ ΡΘ–Ά≥ΤΈΣΙ≈ΒδΗ≈¬ ΡΘ–ΆΘ§Φρ≥ΤΙ≈ΒδΗ≈–Ά:(1) ‘―ι÷–Υυ”–Ω…Ρή≥ωœ÷ΒΡΜυ±Ψ ¬Φΰ÷Μ”–”–œόΗωΘ°(2)ΟΩΗωΜυ±Ψ ¬Φΰ≥ωœ÷ΒΡΩ…Ρή–‘œύΒ»Θ°»γΙϊ“Μ¥Έ ‘―ι÷–Ω…Ρή≥ωœ÷ΒΡΫαΙϊ”–nΗωΘ§Εχ«“Υυ”–ΫαΙϊ≥ωœ÷ΒΡΩ…Ρή–‘ΕΦœύΒ»Θ§Ρ«Ο¥ΟΩ“ΜΗωΜυ±Ψ ¬ΦΰΒΡΗ≈¬ ΕΦ «![]() ΘΜ»γΙϊΡ≥Ηω ¬ΦΰAΑϋά®ΒΡΫαΙϊ”–mΗωΘ§Ρ«Ο¥ ¬ΦΰAΒΡΗ≈¬ P(A)ΘΫ
ΘΜ»γΙϊΡ≥Ηω ¬ΦΰAΑϋά®ΒΡΫαΙϊ”–mΗωΘ§Ρ«Ο¥ ¬ΦΰAΒΡΗ≈¬ P(A)ΘΫ![]() Θ°
Θ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ