题目内容
10.已知数列{an}中a1=1,an+1=$\frac{2{a}_{n}}{{a}_{n}+2}$,求通项公式an.分析 由递推公式求出数列的前4项,总结规律,猜想出数列的通项公式,再用数学归纳法进行证明.
解答 解:∵数列{an}中a1=1,an+1=$\frac{2{a}_{n}}{{a}_{n}+2}$,
∴${a}_{2}=\frac{2×1}{1+2}$=$\frac{2}{3}$,${a}_{3}=\frac{2×\frac{2}{3}}{\frac{2}{3}+2}$=$\frac{1}{2}$=$\frac{2}{4}$,
${a}_{4}=\frac{2×\frac{1}{2}}{\frac{1}{2}+2}$=$\frac{2}{5}$,…
由此猜想an=$\frac{2}{n+1}$.
下面利用数学归纳法证明:
①当n=1时,a1=$\frac{2}{1+1}$=1,成立.
②假设n=k时,成立,即ak=$\frac{2}{k+1}$,
则${a}_{k+1}=\frac{2{a}_{k}}{{a}_{k}+2}$=$\frac{\frac{4}{k+1}}{\frac{2}{k+1}+2}$=$\frac{4}{2+2(k+1)}$=$\frac{2}{(k+1)+1}$,成立,
∴${a}_{n}=\frac{2}{n+1}$.
∴通项公式an=$\frac{2}{n+1}$.
点评 本题考查数列的通项公式的求法,是中档题,解题时要注意合理猜想和数学归纳法的灵活运用.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
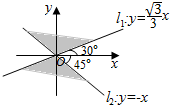 已知角α的终边在如图所示的阴影区域内(包括边界),试求出角α的集合.
已知角α的终边在如图所示的阴影区域内(包括边界),试求出角α的集合.