题目内容
如图,在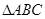 中,
中,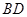 为
为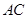 边上的高,
边上的高,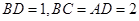 ,沿
,沿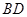 将
将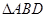 翻折,使得
翻折,使得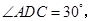 得几何体
得几何体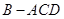
(1)求证: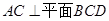 ; (2)求二面角
; (2)求二面角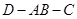 的余弦值。
的余弦值。
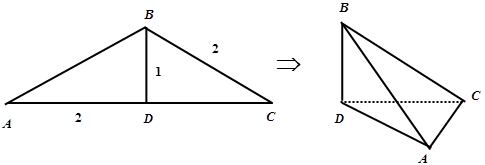
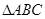 中,
中,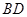 为
为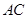 边上的高,
边上的高,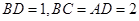 ,沿
,沿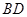 将
将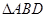 翻折,使得
翻折,使得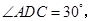 得几何体
得几何体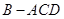
(1)求证:
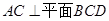 ; (2)求二面角
; (2)求二面角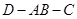 的余弦值。
的余弦值。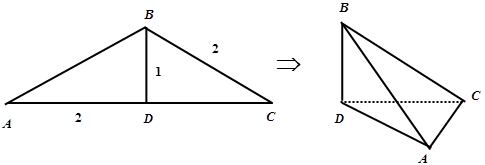
因为 ,所以
,所以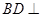 平面
平面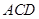 。
。
又因为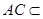 平面
平面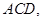 所以
所以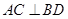 ①……… 1分
①……… 1分
在 中,
中,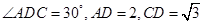 ,由余弦定理,
,由余弦定理,
得
因为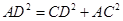 ,所以
,所以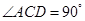 ,即
,即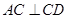 。② ……… 3分
。② ……… 3分
由①,②及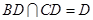 ,可得
,可得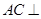 平面
平面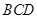 ………4分
………4分
(2)在 中,过
中,过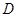 作
作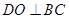 于
于 ,则
,则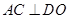 ,所以
,所以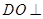 平面
平面
在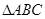 中,过
中,过 作
作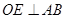 于
于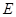 ,连
,连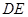 ,则
,则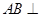 平面
平面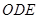 ,
,
所以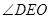 为二面角
为二面角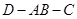 的平面角 ……… 6分
的平面角 ……… 6分
在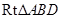 中,求得
中,求得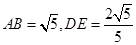 ,
,
在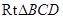 中,求得
中,求得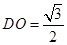 ,
,
所以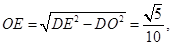 所以
所以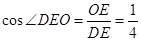 。
。
因此,所求二面角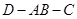 的余弦值为
的余弦值为 。
。
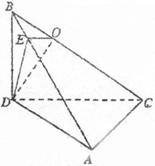
 ,所以
,所以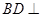 平面
平面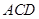 。
。又因为
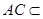 平面
平面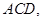 所以
所以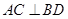 ①……… 1分
①……… 1分在
 中,
中,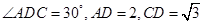 ,由余弦定理,
,由余弦定理,得

因为
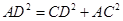 ,所以
,所以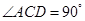 ,即
,即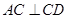 。② ……… 3分
。② ……… 3分由①,②及
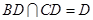 ,可得
,可得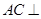 平面
平面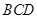 ………4分
………4分(2)在
 中,过
中,过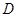 作
作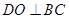 于
于 ,则
,则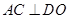 ,所以
,所以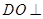 平面
平面
在
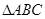 中,过
中,过 作
作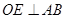 于
于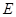 ,连
,连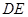 ,则
,则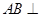 平面
平面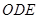 ,
,所以
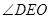 为二面角
为二面角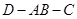 的平面角 ……… 6分
的平面角 ……… 6分在
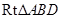 中,求得
中,求得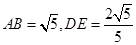 ,
,在
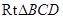 中,求得
中,求得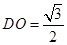 ,
,所以
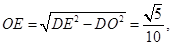 所以
所以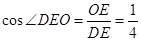 。
。因此,所求二面角
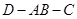 的余弦值为
的余弦值为 。
。
略

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 ,
, ,则
,则 ,
, 两点间的距离是
两点间的距离是


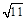
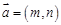 ,
,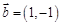 ,其中
,其中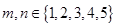 ,则
,则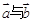 的夹角能成为直角三角形内角的概率是
的夹角能成为直角三角形内角的概率是 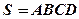 中,
中,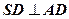 ,
,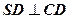 ,
,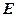 是
是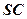 的中点,
的中点,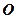 是底面正方形
是底面正方形 的中心,
的中心,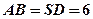 。
。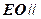 面
面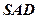 ;
;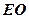 与平面
与平面
 ,
, ,
, ,且
,且 ,则
,则 .
. 关于
关于 轴的对称点是B
轴的对称点是B ,则
,则 的值依次是( )
的值依次是( )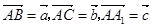 ,则
,则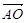 = ▲ .(试用
= ▲ .(试用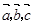 表示)
表示)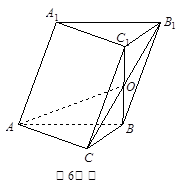
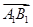 =
=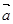 ,
, =
=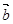 ,
,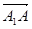 =
=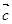 则下列向量中与
则下列向量中与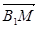 相等的向量是( )
相等的向量是( )
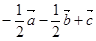

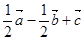
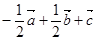
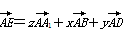 ,则x+y+z的值为( )
,则x+y+z的值为( )