题目内容
在空间直角坐标系中,已知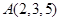 ,
,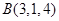 ,则
,则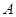 ,
,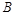 两点间的距离是
两点间的距离是
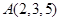 ,
,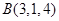 ,则
,则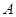 ,
,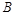 两点间的距离是
两点间的距离是A.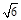 | B.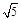 | C.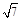 | D. |
A
试题分析:∵A,B两点的坐标分别是A(2,3,5),B(3,1,4),
∴|AB|=
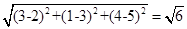 。故选A.
。故选A.点评:本题考查空间两点之间的距离公式,是一个基础题,这种题目是一些解析几何问题的题目的一个环节,一般不会单独出题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
题目内容
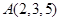 ,
,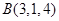 ,则
,则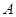 ,
,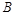 两点间的距离是
两点间的距离是A.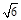 | B.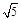 | C.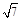 | D. |
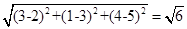 。故选A.
。故选A.
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案