题目内容
已知椭圆C: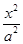 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为 .
.
(1)求椭圆C的方程;
(2)已知动直线y=k(x+1)与椭圆C相交于A,B两点.
①若线段AB中点的横坐标为- ,求斜率k的值;
,求斜率k的值;
②已知点M(-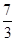 ,0),求证:
,0),求证: ·
· 为定值.
为定值.
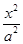 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为 .
.(1)求椭圆C的方程;
(2)已知动直线y=k(x+1)与椭圆C相交于A,B两点.
①若线段AB中点的横坐标为-
 ,求斜率k的值;
,求斜率k的值;②已知点M(-
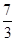 ,0),求证:
,0),求证: ·
· 为定值.
为定值.(1) +
+ =1
=1
(2)①± ②见解析
②见解析
 +
+ =1
=1(2)①±
 ②见解析
②见解析(1)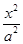 +
+ =1(a>b>0)满足a2=b2+c2,又
=1(a>b>0)满足a2=b2+c2,又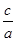 =
= ,
, ×b×2c=
×b×2c= ,
,
解得a2=5,b2= ,则椭圆方程为
,则椭圆方程为 +
+ =1.
=1.
(2)设A(x1,y1),B(x2,y2).
①将y=k(x+1)代入 +
+ =1,
=1,
得(1+3k2)x2+6k2x+3k2-5=0,
∴Δ=48k2+20>0,x1+x2=- ,
,
∵AB中点的横坐标为- ,
,
∴- =-1,解得k=±
=-1,解得k=± .
.
②由(1)知x1+x2=- ,x1x2=
,x1x2= ,
,
∴ ·
· =(x1+
=(x1+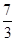 ,y1)·(x2+
,y1)·(x2+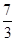 ,y2)
,y2)
=(x1+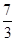 )(x2+
)(x2+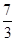 )+y1y2
)+y1y2
=(x1+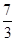 )(x2+
)(x2+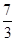 )+k2(x1+1)(x2+1)
)+k2(x1+1)(x2+1)
=(1+k2)x1x2+(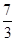 +k2)(x1+x2)+
+k2)(x1+x2)+ +k2
+k2
=(1+k2) +(
+(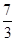 +k2)(-
+k2)(- )+
)+ +k2
+k2
= +
+ +k2=
+k2= (定值).
(定值).
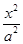 +
+ =1(a>b>0)满足a2=b2+c2,又
=1(a>b>0)满足a2=b2+c2,又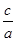 =
= ,
, ×b×2c=
×b×2c= ,
,解得a2=5,b2=
 ,则椭圆方程为
,则椭圆方程为 +
+ =1.
=1.(2)设A(x1,y1),B(x2,y2).
①将y=k(x+1)代入
 +
+ =1,
=1,得(1+3k2)x2+6k2x+3k2-5=0,
∴Δ=48k2+20>0,x1+x2=-
 ,
,∵AB中点的横坐标为-
 ,
,∴-
 =-1,解得k=±
=-1,解得k=± .
.②由(1)知x1+x2=-
 ,x1x2=
,x1x2= ,
,∴
 ·
· =(x1+
=(x1+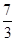 ,y1)·(x2+
,y1)·(x2+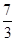 ,y2)
,y2)=(x1+
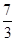 )(x2+
)(x2+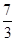 )+y1y2
)+y1y2=(x1+
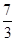 )(x2+
)(x2+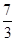 )+k2(x1+1)(x2+1)
)+k2(x1+1)(x2+1)=(1+k2)x1x2+(
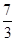 +k2)(x1+x2)+
+k2)(x1+x2)+ +k2
+k2=(1+k2)
 +(
+(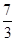 +k2)(-
+k2)(- )+
)+ +k2
+k2=
 +
+ +k2=
+k2= (定值).
(定值).
练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 +
+ =1(a>b>0)的左、右顶点,(1,)为椭圆上一点,椭圆长半轴长等于焦距.
=1(a>b>0)的左、右顶点,(1,)为椭圆上一点,椭圆长半轴长等于焦距.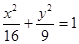 的焦点为顶点,以该椭圆的顶点为焦点的双曲线方程是 .
的焦点为顶点,以该椭圆的顶点为焦点的双曲线方程是 . 上的点M与椭圆右焦点
上的点M与椭圆右焦点 的连线
的连线 与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
 的面积是
的面积是 ,求此时椭圆的方程.
,求此时椭圆的方程.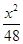 +
+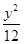 =1交于点E,F,则△OEF(O为坐标原点)的面积为( )
=1交于点E,F,则△OEF(O为坐标原点)的面积为( )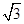
 +y2=1的两个焦点为F1,F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则|PF2|=( )
+y2=1的两个焦点为F1,F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则|PF2|=( )


 的右焦点重合,则该抛物线的准线方程为___________.
的右焦点重合,则该抛物线的准线方程为___________. 、
、 ,且
,且 是
是 与
与 的等差中项,则动点
的等差中项,则动点 的轨迹方程是( )
的轨迹方程是( )