题目内容
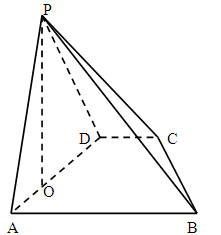
如图,在四棱锥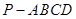 中,底面
中,底面 是直角梯形,
是直角梯形,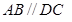 ,
, ,
,
平面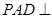 平面
平面 ,若
,若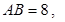
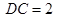 ,
,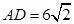 ,
, ,
,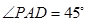 ,且
,且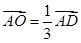 .
.
(1)求证: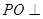 平面
平面 ;
;
(2)设平面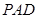 与平面
与平面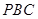 所成二面角的大小为
所成二面角的大小为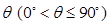 ,求
,求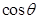 的值.
的值.
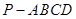 中,底面
中,底面 是直角梯形,
是直角梯形,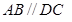 ,
, ,
,平面
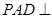 平面
平面 ,若
,若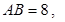
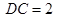 ,
,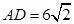 ,
, ,
,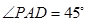 ,且
,且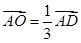 .
.
(1)求证:
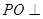 平面
平面 ;
; (2)设平面
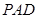 与平面
与平面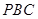 所成二面角的大小为
所成二面角的大小为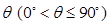 ,求
,求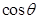 的值.
的值.(1)参考解析;(2)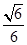
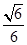
试题分析:(1)由
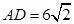 ,
,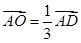 所以
所以 .又
.又 ,
,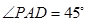 .在三角形PAO中由余弦定理可得
.在三角形PAO中由余弦定理可得 .所以
.所以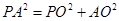 .即
.即 .又平面
.又平面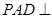 平面
平面 且平面
且平面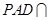 平面
平面 =AD,
=AD,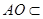 平面PAD.所以
平面PAD.所以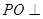 平面
平面 .
.(2)由题意可得建立空间坐标系,写出相应点的坐标,平面PAD的法向量易得,用待定系数写出平面PBC的法向量,根据两向量的法向量夹角的余弦值,求出二面角的余弦值.
(1)因为
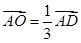 ,
,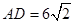 ,所以
,所以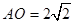 , 1分
, 1分在
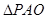 中,由余弦定理
中,由余弦定理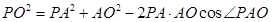 ,
,得
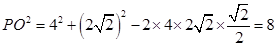 , 3分
, 3分 ,
, , 4分
, 4分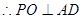 , 5分
, 5分又
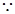 平面
平面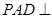 平面
平面 ,平面
,平面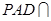 平面
平面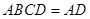 ,
,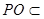 平面
平面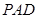 ,
, 平面
平面 . 6分
. 6分
(2)如图,过
 作
作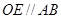 交
交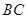 于
于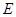 ,则
,则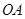 ,
,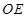 ,
, 两两垂直,以
两两垂直,以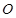 为坐标原点,分别以
为坐标原点,分别以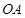 ,
,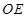 ,
, 所在直线为
所在直线为 轴,建立空间直角坐标系
轴,建立空间直角坐标系 , 7分
, 7分则
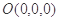 ,
, ,
,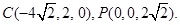 8分
8分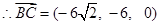 ,
,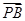
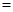
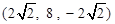 , 9分
, 9分设平面
 的一个法向量为
的一个法向量为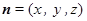 ,
,由
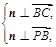
 得
得 即
即
取
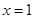 则
则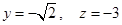 ,
,所以
 为平面
为平面 的一个法向
的一个法向量. 11分
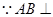 平面
平面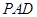 ,
, 为平面
为平面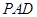 的
的一个法向量.
所以

 , 12分
, 12分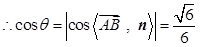 . 13分
. 13分
练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 中,
中, ,
, 分别为边
分别为边 和
和 上的点,且
上的点,且 ,
, .将四边形
.将四边形 沿
沿 折起成如图2的位置,使
折起成如图2的位置,使 .
.
 平面
平面 ;
; 所成锐角的余弦值.
所成锐角的余弦值.
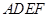 与梯形
与梯形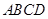 所在的平面互相垂直,
所在的平面互相垂直,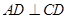 ,
,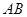 ∥
∥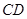 ,
,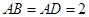 ,
,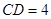 ,
,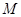 为
为 的中点.
的中点.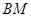 ∥平面
∥平面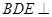 平面
平面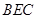 ;
;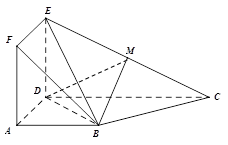
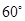 ,∠BAC
,∠BAC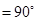 ,AD是BC上的高,沿AD把△ABD折起,使∠BDC
,AD是BC上的高,沿AD把△ABD折起,使∠BDC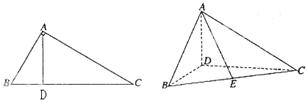
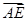 与
与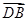 夹角的余弦值.
夹角的余弦值.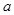 .
.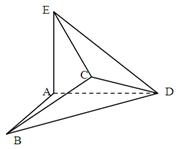
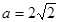 ,求证:AB∥平面CDE;
,求证:AB∥平面CDE; 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )
中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )