题目内容
如图,将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=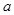 .
.
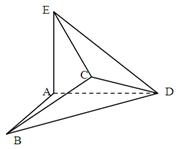
(1)若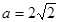 ,求证:AB∥平面CDE;
,求证:AB∥平面CDE;
(2)求实数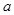 的值,使得二面角AECD的大小为60°.
的值,使得二面角AECD的大小为60°.
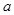 .
.
(1)若
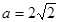 ,求证:AB∥平面CDE;
,求证:AB∥平面CDE;(2)求实数
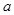 的值,使得二面角AECD的大小为60°.
的值,使得二面角AECD的大小为60°.(1)答案详见解析;(2)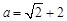
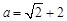
试题分析:空间向量在立体几何中的应用,最大的优点就是避开了传统立体几何中“如何添加辅助线”这个难点,使得操作更模式化、易操作.需根据已知条件寻找(或添加)三条共点的两两垂直的三条垂线,分别作为
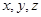 轴,建立空间直角坐标系.(1)由已知,以
轴,建立空间直角坐标系.(1)由已知,以 的方向作为
的方向作为 轴的正方向,建立如图所示的空间直角坐标系,用坐标表示有关点,要证明AB∥平面CDE,只需证明
轴的正方向,建立如图所示的空间直角坐标系,用坐标表示有关点,要证明AB∥平面CDE,只需证明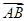 垂直于面CDE的法向量即可.本题还可以利用线面垂直的判定定理证明;(2)分别求出面
垂直于面CDE的法向量即可.本题还可以利用线面垂直的判定定理证明;(2)分别求出面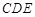 和面
和面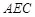 的法向量,并求法向量的夹角,利用余弦值等于
的法向量,并求法向量的夹角,利用余弦值等于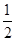 列方程,求
列方程,求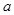 即可.
即可.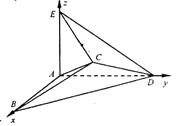
试题解析:(1)如图建立空间指教坐标系,则A(0,0,0),B(2,0,0),C(1,1,
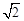 ),D(0,2,0),E(0,0,
),D(0,2,0),E(0,0, ),
),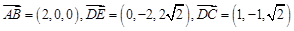 2分
2分设平面
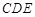 的一个法向量为
的一个法向量为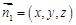 ,
,则有
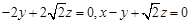 ,
,取
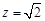 时,
时,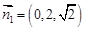 4分
4分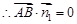 ,又
,又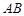 不在平面
不在平面 内,所以
内,所以 平面
平面 ; 7分
; 7分(2)如图建立空间直角坐标系,则
A(0,0,0),B(2,0,0),C(1,1,
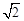 ),D(0,2,0),E(0,0,
),D(0,2,0),E(0,0,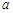 ),
),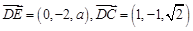 ,
,设平面
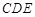 的一个法向量为
的一个法向量为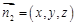 ,
,则有
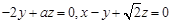 ,取
,取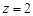 时,
时,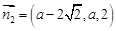 9分
9分又平面
 的一个法向量为
的一个法向量为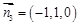 , 10分
, 10分因为二面角
 的大小为
的大小为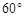 ,
,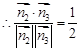 ,
,即
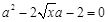 ,解得
,解得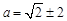 14分
14分又
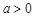 ,所以
,所以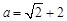 . 15分
. 15分
练习册系列答案
相关题目
 中,底面
中,底面 是直角梯形,
是直角梯形,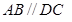 ,
, ,
,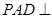 平面
平面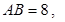
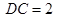 ,
,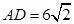 ,
, ,
,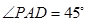 ,且
,且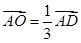 .
.
 平面
平面 与平面
与平面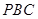 所成二面角的大小为
所成二面角的大小为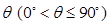 ,求
,求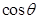 的值.
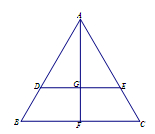
的值.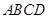 为平行四边形,
为平行四边形,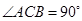 ,
,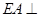 平面
平面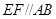 ,
,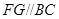 ,
,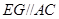 ,
,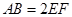 .
.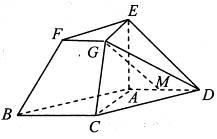
 是线段
是线段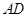 的中点,求证:
的中点,求证: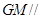 平面
平面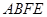 ;
;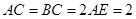 ,求二面角
,求二面角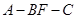 的余弦值.
的余弦值.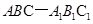 ,
,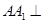 平面
平面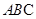 ,
, ,
,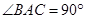 ,四边形
,四边形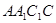 为正方形,
为正方形,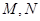 分别为
分别为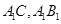 中点.
中点.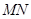 ∥面
∥面 ;
; —
— —
— 的余弦值.
的余弦值.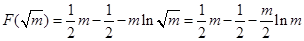 沿AF折起,得到如图所示的三棱锥
沿AF折起,得到如图所示的三棱锥 ,其中
,其中 .
.
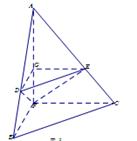
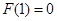 //平面
//平面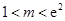 ;
;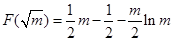 ;
;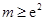 时,求三棱锥
时,求三棱锥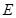 是以
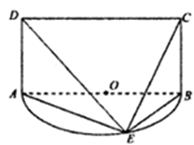
是以 为直径的半圆
为直径的半圆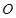 上异于
上异于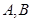 的点,矩形
的点,矩形 所在的平面垂直于半圆
所在的平面垂直于半圆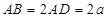 。
。
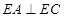 。
。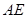 和
和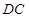 所成的角为
所成的角为 ,求平面
,求平面 和平面
和平面 所成的锐二面角的余弦值。
所成的锐二面角的余弦值。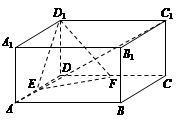
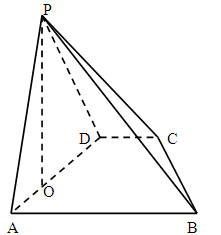
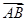 =a,
=a,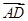 =b,
=b,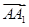 =c,则
=c,则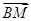 =________.
=________.