题目内容
已知函数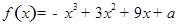 在区间[-2,2]的最大值为20,求它在该区间的最小值。
在区间[-2,2]的最大值为20,求它在该区间的最小值。
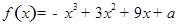 在区间[-2,2]的最大值为20,求它在该区间的最小值。
在区间[-2,2]的最大值为20,求它在该区间的最小值。最小值为-7.
试题分析:因为
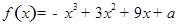 ,所以
,所以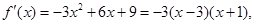
令
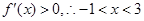 ,
,所以该函数在
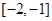 上单调递减,在
上单调递减,在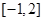 上单调递增,
上单调递增,所以函数在
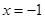 处取到最小值,
处取到最小值,而
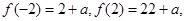
所以该函数在区间[-2,2]的最大值为
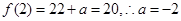 ,
,所以该函数在区间[-2,2]的最小值为
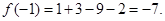
点评:解决此类问题的关键是利用导数研究单调性、极值、最值等,要交代清楚函数的单调性,必要时可以借助表格进行说明.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目

 时,求函数
时,求函数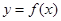 在点
在点 处的切线方程;
处的切线方程;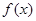 在
在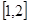 上是减函数,求实数
上是减函数,求实数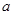 的取值范围;
的取值范围;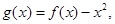 是否存在实数
是否存在实数 是自然对数的底)时,函数
是自然对数的底)时,函数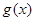 的最小值是3,
的最小值是3,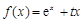 (e为自然对数的底数).
(e为自然对数的底数).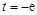 时,求函数
时,求函数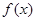 的单调区间;
的单调区间;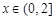 ,不等式
,不等式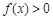 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.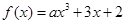 有极值,
有极值, 的取值范围;
的取值范围;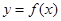 的导函数
的导函数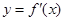 的图象,对此图象,有如下结论:
的图象,对此图象,有如下结论: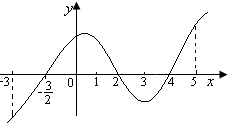
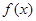 是增函数;
是增函数;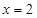 时,
时,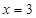 时,
时, ,设函数
,设函数

 ,求函数
,求函数 在
在 上的最小值
上的最小值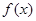 在R上可导,且
在R上可导,且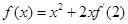 ,则
,则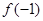 与
与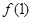 的大小为( )
的大小为( )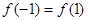
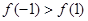
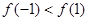
 在
在 处有极值,其图象在
处有极值,其图象在 处的切线与直线
处的切线与直线 平行.
平行. 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。