题目内容
已知函数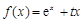 (e为自然对数的底数).
(e为自然对数的底数).
(Ⅰ)当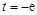 时,求函数
时,求函数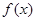 的单调区间;
的单调区间;
(Ⅱ)若对于任意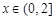 ,不等式
,不等式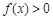 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
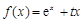 (e为自然对数的底数).
(e为自然对数的底数).(Ⅰ)当
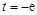 时,求函数
时,求函数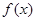 的单调区间;
的单调区间;(Ⅱ)若对于任意
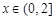 ,不等式
,不等式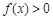 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.(1)函数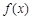 的单调递增区间是
的单调递增区间是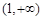 ;单调递减区间是
;单调递减区间是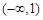
(2)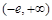 .
.
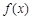 的单调递增区间是
的单调递增区间是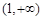 ;单调递减区间是
;单调递减区间是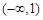
(2)
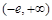 .
.试题分析:(1),根据题意,由于函数
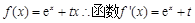
当t=-e时,即导数为
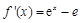 ,
,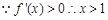 ,函数
,函数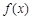 的单调递增区间是
的单调递增区间是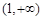 ;
;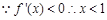 单调递减区间是
单调递减区间是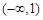
(2) 根据题意由于对于任意
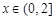 ,不等式
,不等式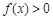 恒成立,则在第一问的基础上,由于函数
恒成立,则在第一问的基础上,由于函数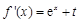 ,只要求解函数的最小值大于零即可,由于当t>0,函数子啊R递增,没有最小值,当t<0,那么可知
,只要求解函数的最小值大于零即可,由于当t>0,函数子啊R递增,没有最小值,当t<0,那么可知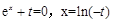 ,那么在给定的区间上可知当x=ln(-t)时取得最小值为2,
,那么在给定的区间上可知当x=ln(-t)时取得最小值为2,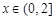 那么可知t的取值范围是
那么可知t的取值范围是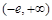 .
.点评:主要是考查了导数的运用,以及函数最值的运用,属于中档题。

练习册系列答案
相关题目
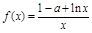 ,
,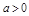 .
.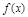 的极值;
的极值;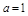 时,若不等式
时,若不等式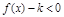 在
在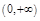 上恒成立,求
上恒成立,求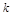 的取值范围.
的取值范围.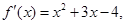 则
则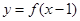 的单调减区间( )
的单调减区间( )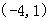
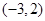
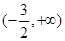
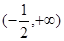
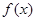 的导函数为
的导函数为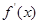 ,对任意
,对任意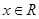 都有
都有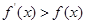 成立,则( )
成立,则( )
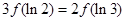
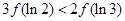
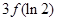 与
与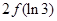 的大小不确定
的大小不确定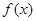 具有下列特征:
具有下列特征: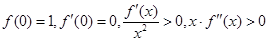 ,则
,则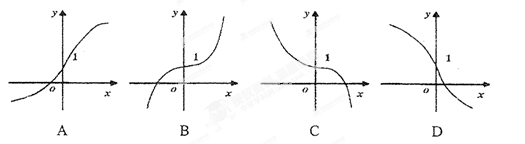
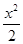 -aln(x+1),a∈R.
-aln(x+1),a∈R.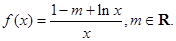
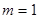 ,判断函数在定义域内的单调性;
,判断函数在定义域内的单调性;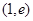 内存在极值,求实数m的取值范围。
内存在极值,求实数m的取值范围。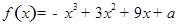 在区间[-2,2]的最大值为20,求它在该区间的最小值。
在区间[-2,2]的最大值为20,求它在该区间的最小值。
 ,求
,求 的单调区间;
的单调区间; ≥0时
≥0时 的取值范围.
的取值范围.