题目内容
10.已知ex+ax-a>0恒成立,则实数a的取值范围为(-e2,0].分析 由题意可得ex>-a(x-1),当x=1,x>1,x<1时,运用参数分离和导数,求得单调性,解不等式即可得到所求范围.
解答 解:ex+ax-a>0恒成立,
即为ex>-a(x-1),
当x=1时,e>0成立;
当x>1时,-a<$\frac{{e}^{x}}{x-1}$的最小值,
由f(x)=$\frac{{e}^{x}}{x-1}$的导数为f′(x)=$\frac{{e}^{x}(x-2)}{(x-1)^{2}}$,
当x=2时,f(x)取得最小值e2,
即有-a<e2,解得a>-e2;
当x<1时,-a>$\frac{{e}^{x}}{x-1}$,
由f(x)=$\frac{{e}^{x}}{x-1}$的导数为f′(x)=$\frac{{e}^{x}(x-2)}{(x-1)^{2}}$<0,
f(x)递减,即有f(x)<0,
即有-a≥0,解得a≤0.
则a的范围是(-e2,0].
点评 本题考查不等式恒成立问题的解法,注意运用参数分离和换元法,运用导数判断单调性求得最值,考查运算能力,属于中档题.

练习册系列答案
相关题目
5.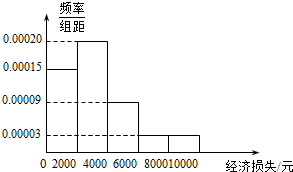 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图:
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图:
(Ⅰ)试根据频率分布直方图估计小区平均每户居民的平均损失(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)小明向班级同学发出倡议,为该小区居民捐款.现从损失超过4000元的居民中随机抽出2户进行捐款援助,设抽出损失超过8000元的居民为ξ户,求ξ的分布列和数学期望;
(Ⅲ)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如下表,在表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
附:临界值表参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.
 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图:
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图:(Ⅰ)试根据频率分布直方图估计小区平均每户居民的平均损失(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)小明向班级同学发出倡议,为该小区居民捐款.现从损失超过4000元的居民中随机抽出2户进行捐款援助,设抽出损失超过8000元的居民为ξ户,求ξ的分布列和数学期望;
(Ⅲ)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如下表,在表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
| 经济损失不超过 4000元 | 经济损失超过 4000元 | 合计 | |
| 捐款超过 500元 | 30 | ||
| 捐款不超 过500元 | 6 | ||
| 合计 | (图2) |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
15.集合A={x|(x-1)(x+2)<0},集合B={x|lgx≤0},则A∩B=( )
| A. | (0,1) | B. | (0,1] | C. | (-2,1] | D. | (-2,1) |
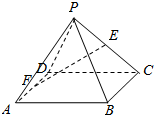 如图,四棱锥P-ABCD中,ABCD为矩形,面PDC⊥面ABCD,∠DPC=90°,E,F 分别为PC,AD的中点.
如图,四棱锥P-ABCD中,ABCD为矩形,面PDC⊥面ABCD,∠DPC=90°,E,F 分别为PC,AD的中点.