题目内容
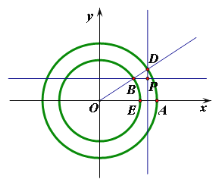
【题目】已知直线
，斜率为
的直线
与x轴交于点A，与y轴交于点
，过
作x 轴的平行线，交
于点
，过作y轴的平行线，交于点
，再过作x轴的平行线交于点
，…，这样依次得线段
、
、
、
、…、
、
，记
为点
的横坐标，则
__________．
【答案】
【解析】
先由题设条件得出点
的坐标，根据它们之间的关系求出点
的坐标，然后利用数列极限的运算性质求出
.
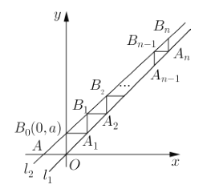
解：∵斜率为
的直线
与x轴交于点A，与y轴交于点
，直线
，
∴A1（a，a）.
∵A1B0∥x轴，∴B1（a，aq+a），A2（aq+a，aq+a）.
∵B1A2∥x轴，∴B2（aq+a，aq2+aq+a）.
同理可得：A3（aq2+aq+a，aq2+aq+a），
B3（aq2+aq+a，aq3+aq2+aq+a），…，
Bn（aqn﹣1+aqn﹣2+aqn﹣3+…aq2+aq+a，aqn+aqn﹣1+aqn﹣2+aqn﹣3+…aq2+aq+a），
∵xn为点Bn的横坐标，
∴xn＝aqn﹣1+aqn﹣2+aqn﹣3+…aq2+aq+a.
故xn是首项为a，公比为q（0＜q＜1）的等比数列的前n项的和，
由数列极限的运算性质得：
.
故答案为：.
练习册系列答案
相关题目
