Question

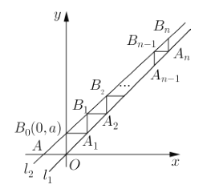
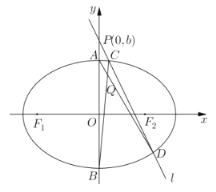
【题目】在平面直角坐标系中，A、B分别为椭圆的上、下顶点，若动直线l过点，且与椭圆相交于C、D两个不同点（直线l与y轴不重合，且C、D两点在y轴右侧，C在D的上方），直线AD与BC相交于点Q．

（1）设的两焦点为、，求的值;

（2）若，且，求点Q的横坐标；

（3）是否存在这样的点P，使得点Q的纵坐标恒为？若存在，求出点P的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）（2）；（3）

【解析】

（1）由椭圆方程易知∠OAF2＝45°，结合对称性可得∠F1AF2＝90°；
（2）设C（x1，y1），D（x2，y2），根据已知条件可求得直线BC的方程为y＝2x﹣1，直线AD的方程为y＝﹣x+1，联立两直线方程即可得到点Q的横坐标；
（3）设直线l的方程为y＝kx+b（k＜0，b＞1），与椭圆方程联立，可得，直线BC的方程为，直线AD的方程为，进而得到点Q的纵坐标，由此建立方程化简即可得出结论.

解：（1）由椭圆Γ的方程知，F1（﹣1，0），F2（1，0），A（0，1），

则∠OAF2＝45°，

∴∠F1AF2＝90°；

（2）若b＝3，设C、D的两点坐标为C（x1，y1），D（x2，y2），

∵，

∴，即，

而C（x1，y1），D（x2，y2）均在上，

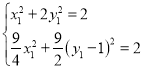代入得，解得，

∴，分别代入Γ解得，，

∴直线BC的方程为y＝2x﹣1，直线AD的方程为y＝﹣x+1，

联立，解得，

∴Q点的横坐标为；

（3）假设存在这样的点P，设直线l的方程为y＝kx+b（k＜0，b＞1），

点C，D的坐标为C（x1，y1），D（x2，y2），

联立，得（2k2+1）x2+4kbx+2b2﹣2＝0，

由△＝16k2b2﹣8（2k2+1）（b2﹣1）＞0，得，

由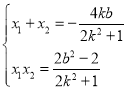，可得，

直线BC的方程为，直线AD的方程为，

而x1y2＝kx1x2+bx1，x2y1＝kx1x2+bx2，联立，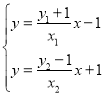

得

＝，

则b＝3＞1，因此，存在点P（0，3），使得点Q的纵坐标恒为.