题目内容
【题目】如图，抛物线
的焦点为
，过点
作直线
与抛物线交于
、
两点，当直线与
轴垂直时
长为
.
（1）求抛物线的方程；
（2）若
与
的面积相等，求直线的方程.
【答案】（1）
；（2）
或
.
【解析】
（1）由题意可知点
在抛物线
上，将该点坐标代入抛物线的方程，求得
的值，进而可求得抛物线的方程；
（2）由题意得出
，可得知直线
的斜率不为零，可设直线的方程为
，将该直线方程与抛物线方程连理，列出韦达定理，由题意得出
，代入韦达定理后可求得
的值，进而可求得直线的方程.
（1）当直线
与
轴垂直时的长为
，
又
，取
，所以
，解得
，
所以抛物线的方程为；
（2）由题意知
，
，
因
，所以，
当
时，直线与抛物线不存在两个交点，所以
，
故设直线的方程为，代入抛物线方程得
，
所以
，
，
，
可得
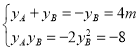，解得
.
所以，直线的方程为或.
应用题作业本系列答案【题目】某班级有60名学生，学号分别为1～60，其中男生35人，女生25人．为了了解学生的体质情况，甲、乙两人对全班最近一次体育测试的成绩分别进行了随机抽样．其中一人用的是系统抽样，另一人用的是分层抽样，他们得到各12人的样本数据如下所示，并规定体育成绩大于或等于80人为优秀．
甲抽取的样本数据：
学号 | 4 | 9 | 14 | 19 | 24 | 29 | 34 | 39 | 44 | 49 | 54 | 59 |
性别 | 男 | 女 | 男 | 男 | 女 | 男 | 女 | 男 | 女 | 女 | 男 | 男 |
体育成绩 | 90 | 80 | 75 | 80 | 83 | 85 | 75 | 80 | 70 | 80 | 83 | 70 |
女抽取的样本数据：
学号 | 1 | 8 | 10 | 20 | 23 | 28 | 33 | 35 | 43 | 48 | 52 | 57 |
性别 | 男 | 男 | 男 | 男 | 男 | 男 | 男 | 女 | 女 | 女 | 女 | 女 |
体育成绩 | 95 | 85 | 85 | 80 | 70 | 80 | 80 | 65 | 70 | 60 | 70 | 80 |
（Ⅰ）在乙抽取的样本中任取4人，记这4人中体育成绩优秀的学生人数为
，求的分布列和数学期望；
（Ⅱ）请你根据乙抽取的样本数据，判断是否有95%的把握认为体育成绩是否为优秀和性别有关；
（Ⅲ）判断甲、乙各用的何种抽样方法，并根据（Ⅱ）的结论判断哪种抽样方法更优，说明理由．
附：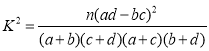
| 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
