题目内容
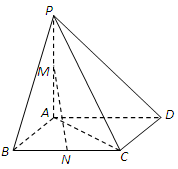
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=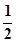 AD=1,CD=
AD=1,CD=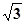 .
.
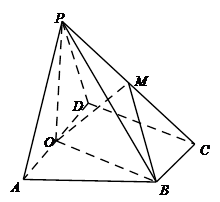
(Ⅰ)求证:平面PQB⊥平面PAD;
(Ⅱ)设PM="t" MC,若二面角M-BQ-C的平面角的大小为30°,试确定t的值.
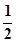 AD=1,CD=
AD=1,CD=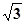 .
.
(Ⅰ)求证:平面PQB⊥平面PAD;
(Ⅱ)设PM="t" MC,若二面角M-BQ-C的平面角的大小为30°,试确定t的值.
(Ⅰ)见解析(Ⅱ)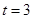
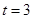
本题考查平面与平面垂直的证明,求实数的取值.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意合理地进行等价转化,合理地运用向量法进行解题.
(Ⅰ)法一:由AD∥BC,BC=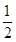 AD,Q为AD的中点,知四边形BCDQ为平行四边形,故CD∥BQ.由∠ADC=90°,知QB⊥AD.由平面PAD⊥平面ABCD,知BQ⊥平面PAD.由此能够证明平面PQB⊥平面PAD.
AD,Q为AD的中点,知四边形BCDQ为平行四边形,故CD∥BQ.由∠ADC=90°,知QB⊥AD.由平面PAD⊥平面ABCD,知BQ⊥平面PAD.由此能够证明平面PQB⊥平面PAD.
法二:由AD∥BC,BC=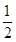
AD,Q为AD的中点,知四边形BCDQ为平行四边形,故CD∥BQ.由∠ADC=90°,知∠AQB=90°.由PA=PD,知PQ⊥AD,故AD⊥平面PBQ.由此证明平面PQB⊥平面PAD.
(Ⅱ)由PA=PD,Q为AD的中点,知PQ⊥AD.由平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,知PQ⊥平面ABCD.以Q为原点建立空间直角坐标系,利用向量法能够求出t=3.
解:(I)方法一∵AD // BC,BC=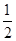 AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD // BQ .
AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD // BQ .
∵∠ADC=90° ∴∠AQB=90° 即QB⊥AD.又
∵平面PAD⊥平面ABCD 且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.∵BQ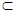 平面PQB,∴平面PQB⊥平面PAD. ……………………6分
平面PQB,∴平面PQB⊥平面PAD. ……………………6分
方法二:AD // BC,BC=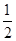 AD,Q为AD的中点, ∴ 四边形BCDQ为平行四边形,∴CD // BQ .
AD,Q为AD的中点, ∴ 四边形BCDQ为平行四边形,∴CD // BQ .
∵ ∠ADC=90° ∴∠AQB=90°. ∵ PA=PD, ∴PQ⊥AD.
∵ PQ∩BQ=Q,∴AD⊥平面PBQ. ∵ AD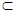 平面PAD,∴平面PQB⊥平面PAD.…………6分
平面PAD,∴平面PQB⊥平面PAD.…………6分
(II)∵PA=PD,Q为AD的中点, ∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
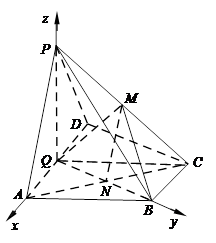
如图,以Q为原点建立空间直角坐标系.
则平面BQC的法向量为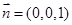 ;
;
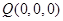 ,
,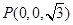 ,
,
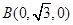 ,
,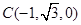 .
.
设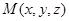 ,则
,则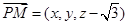 ,
,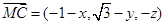 ,
,
∵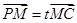 ,
,
∴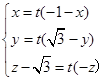 ,
,
∴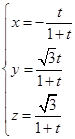 ………………9分
………………9分
在平面MBQ中,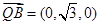 ,
,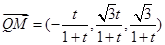 ,
,
∴ 平面MBQ法向量为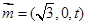 .
.
∵二面角M-BQ-C为30°,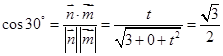 ,
,
∴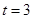 . …………………………12分
. …………………………12分
(Ⅰ)法一:由AD∥BC,BC=
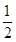 AD,Q为AD的中点,知四边形BCDQ为平行四边形,故CD∥BQ.由∠ADC=90°,知QB⊥AD.由平面PAD⊥平面ABCD,知BQ⊥平面PAD.由此能够证明平面PQB⊥平面PAD.
AD,Q为AD的中点,知四边形BCDQ为平行四边形,故CD∥BQ.由∠ADC=90°,知QB⊥AD.由平面PAD⊥平面ABCD,知BQ⊥平面PAD.由此能够证明平面PQB⊥平面PAD.法二:由AD∥BC,BC=
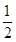
AD,Q为AD的中点,知四边形BCDQ为平行四边形,故CD∥BQ.由∠ADC=90°,知∠AQB=90°.由PA=PD,知PQ⊥AD,故AD⊥平面PBQ.由此证明平面PQB⊥平面PAD.
(Ⅱ)由PA=PD,Q为AD的中点,知PQ⊥AD.由平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,知PQ⊥平面ABCD.以Q为原点建立空间直角坐标系,利用向量法能够求出t=3.
解:(I)方法一∵AD // BC,BC=
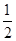 AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD // BQ .
AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD // BQ . ∵∠ADC=90° ∴∠AQB=90° 即QB⊥AD.又
∵平面PAD⊥平面ABCD 且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.∵BQ
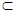 平面PQB,∴平面PQB⊥平面PAD. ……………………6分
平面PQB,∴平面PQB⊥平面PAD. ……………………6分方法二:AD // BC,BC=
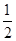 AD,Q为AD的中点, ∴ 四边形BCDQ为平行四边形,∴CD // BQ .
AD,Q为AD的中点, ∴ 四边形BCDQ为平行四边形,∴CD // BQ .∵ ∠ADC=90° ∴∠AQB=90°. ∵ PA=PD, ∴PQ⊥AD.
∵ PQ∩BQ=Q,∴AD⊥平面PBQ. ∵ AD
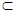 平面PAD,∴平面PQB⊥平面PAD.…………6分
平面PAD,∴平面PQB⊥平面PAD.…………6分(II)∵PA=PD,Q为AD的中点, ∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.

则平面BQC的法向量为
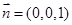 ;
;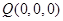 ,
,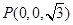 ,
,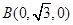 ,
,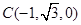 .
. 设
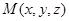 ,则
,则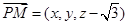 ,
,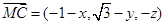 ,
,∵
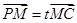 ,
,∴
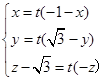 ,
, ∴
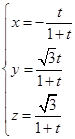 ………………9分
………………9分在平面MBQ中,
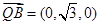 ,
,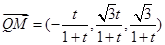 ,
,∴ 平面MBQ法向量为
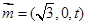 .
. ∵二面角M-BQ-C为30°,
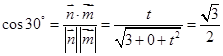 ,
,∴
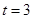 . …………………………12分
. …………………………12分
练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 的底面
的底面 是矩形,
是矩形, ⊥平面
⊥平面 ,
,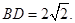

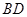 ⊥平面
⊥平面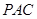 ;
;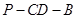 的大小;
的大小; 到平面
到平面 的距离.
的距离.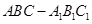 中,所有的棱长都为2,
中,所有的棱长都为2, .
.
 ;
;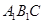 与平面
与平面 所成的锐角的余弦值.
所成的锐角的余弦值.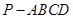 中,底面
中,底面 是矩形,
是矩形,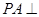 平面
平面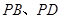 与平面
与平面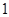 和
和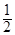 ,
,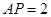 ,
,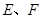 依次是
依次是 的中点.
的中点. ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.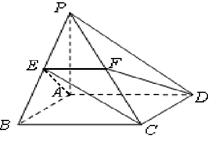
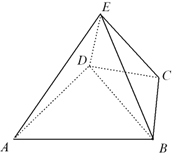
 是四棱锥,△
是四棱锥,△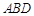 为正三角形,
为正三角形,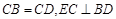 .
.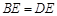 ;
;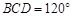 ,M为线段AE的中点,求证:
,M为线段AE的中点,求证: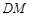 ∥平面
∥平面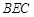 .
.
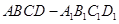 中,侧面
中,侧面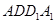 ⊥底面
⊥底面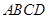 ,
, ,底面
,底面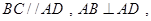
 ,O为
,O为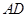 中点.
中点.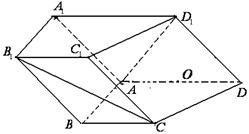
 平面
平面 ;
;

 的棱
的棱 的中点,给出命题
的中点,给出命题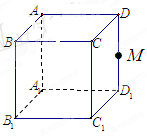
 、
、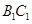 都相交;
都相交;