题目内容
【题目】选修4—4:极坐标与参数方程
在平面直角坐标系![]() 中,将曲线
中,将曲线![]() (
(![]() 为参数) 上任意一点
为参数) 上任意一点![]() 经过伸缩变换
经过伸缩变换 后得到曲线
后得到曲线![]() 的图形.以坐标原点
的图形.以坐标原点![]() 为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线
为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(Ⅱ)点P为曲线![]() 上的任意一点,求点P到直线
上的任意一点,求点P到直线![]() 的距离的最大值及取得最大值时点P的坐标.
的距离的最大值及取得最大值时点P的坐标.
【答案】(1)![]() ,
, ![]() (2)
(2)![]() ,P
,P![]()
【解析】试题分析:(I)根据伸缩变换的公式代入原方程,可以得到伸缩后的曲线方程;
(II)利用点P在椭圆上设出参数坐标,根据点到直线的距离公式求三角函数的最值,并求出取得最值时的![]() 值.
值.
试题解析:(I)由已知有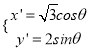 (
(![]() 为参数),消去
为参数),消去![]() 得
得![]() .
.
将![]() 代入直线
代入直线![]() 的方程得
的方程得![]()
![]() 曲线
曲线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的普通方程为
的普通方程为![]() .
.
(II)由(I)可设点![]() 为
为![]() ,
, ![]() .则点
.则点![]() 到直线
到直线![]() 的距离为:
的距离为:
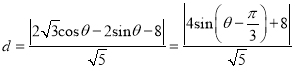
故当![]() ,即
,即![]() 时
时![]() 取最大值
取最大值![]() .
.
span>此时点![]() 的坐标为
的坐标为![]() .
.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案【题目】在某超市,随机调查了100名顾客购物时使用手机支付的情况,得到如下的![]() 列联表,已知其中从使用手机支付的人群中随机抽取1人,抽到青年的概率为
列联表,已知其中从使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
(1)根据已知条件完成![]() 列联表,并根据此资料判断是否有
列联表,并根据此资料判断是否有![]() 的把握认为“超市购物用手机支付与年龄有关”?
的把握认为“超市购物用手机支付与年龄有关”?
(2)现采用分层抽样从这100名顾客中按照“使用手机支付”和“不使用手机支付”中抽取得到一个容量为5的样本,设事件![]() 为“从这个样本中任选3人,这3人中至少有2人是使用手机支付的”,求事件
为“从这个样本中任选3人,这3人中至少有2人是使用手机支付的”,求事件![]() 发生的概率?
发生的概率?
![]() 列联表
列联表
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 28 | ||
合计 | 100 |
|
|
|
|
| 0.001 |
|
|
|
|
| 10.828 |
附:![]()
【题目】近年来,人们对食品安全越来越重视,有机蔬菜的需求也越来越大,国家也制定出台了一系列支持有机肥产业发展的优惠政策,鼓励和引导农民增施有机肥,“藏粮于地,藏粮于技”.根据某种植基地对某种有机蔬菜产量与有机肥用量的统计,每个有机蔬菜大棚产量的增加量![]() (百斤)与使用有机肥料
(百斤)与使用有机肥料![]() (千克)之间对应数据如下表:
(千克)之间对应数据如下表:
使用有机肥料 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
产量增加量 | 2.1 | 2.9 | 3.5 | 4.2 | 4.8 | 5.6 | 6.2 | 6.7 |
(1)根据表中的数据,试建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (精确到
(精确到![]() );
);
(2) 若种植基地每天早上7点将采摘的某有机蔬菜以每千克10元的价格销售到某超市,超市以每千克15元的价格卖给顾客.已知该超市每天8点开始营业,22点结束营业,超市规定:如果当天16点前该有机蔬菜没卖完,则以每千克5元的促销价格卖给顾客(根据经验,当天都能全部卖完).该超市统计了100天该有机蔬菜在每天的16点前的销售量(单位:千克),如表:
每天16点前的 销售量(单位:千克) | 100 | 110 | 120 | 130 | 140 | 150 | 160 |
频数 | 10 | 20 | 16 | 16 | 14 | 14 | 10 |
若以100天记录的频率作为每天16点前销售量发生的概率,以该超市当天销售该有机蔬菜利润的期望值为决策依据,说明该超市选择购进该有机蔬菜110千克还是120千克,能使获得的利润更大?
附:回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为: 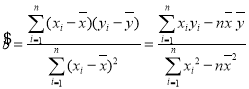 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.