题目内容
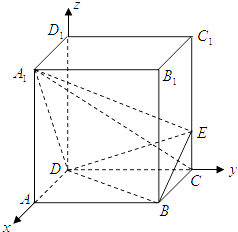
【题目】如图,正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC 
(1)证明:A1C⊥平面BED;
(2)求二面角A1﹣DE﹣B的余弦值.
【答案】
(1)解:如图,以DA,DC,DD1为x,y,z轴,建立空间直角坐标系,
则A1(2,0,4),B(2,2,0),C(0,2,0),D(0,0,0),E(0,2,1)
![]() ,
, ![]() ,
, ![]() ,
,
∵ ![]() ,
,
![]() ,
,
∴ ![]() ,
, ![]() ,
,
∴A1C⊥平面BED
(2)解:∵ ![]() ,
, ![]() ,
,
设平面A1DE的法向量为 ![]() ,
,
由 ![]() 及
及 ![]() ,
,
得﹣2x+2y﹣3z=0,﹣2x﹣4z=0,
取 ![]()
同理得平面BDE的法向量为 ![]() ,
,
∴cos< ![]() >=
>= ![]() =
= ![]() =﹣
=﹣ ![]() ,
,
所以二面角A1﹣DE﹣B的余弦值为 ![]()
【解析】(1)以DA,DC,DD1为x,y,z轴,建立空间直角坐标系,则 ![]() ,
, ![]() ,
, ![]() ,由向量法能证明A1C⊥平面BED.(2)由
,由向量法能证明A1C⊥平面BED.(2)由 ![]() ,
, ![]() ,得到平面A1DE的法向量
,得到平面A1DE的法向量 ![]() ,同理得平面BDE的法向量为
,同理得平面BDE的法向量为 ![]() ,由向量法能求出二面角A1﹣DE﹣B的余弦值.
,由向量法能求出二面角A1﹣DE﹣B的余弦值.
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
画出上表数据的散点图如图所示
(其中  ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() )
)
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() .
.
(2)试根据(1)求出的线性回归方程,预测记忆力为9的学生的判断力
