题目内容
本小题满分12分)
某 次运动会甲、乙两名射击运动员成绩如下:
次运动会甲、乙两名射击运动员成绩如下:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8. 5,1
5,1 0.1,9.2,10.1,9.1;
0.1,9.2,10.1,9.1;
(1)用茎叶图表示甲,乙两个成绩;
(2)分别计算两个样本的平均数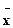 和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定。
和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定。
解:(1)如图所示,茎表示成绩的整数环数,叶表示小数点后的数字。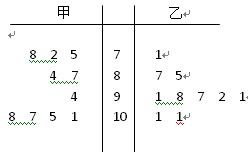 4分
4分
(2)解:(3)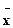 甲=
甲=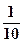 ×(9.4+8.7+7.5+8.4+10.1+10.5+10.7+7.2+7.8+10.8)=9.11
×(9.4+8.7+7.5+8.4+10.1+10.5+10.7+7.2+7.8+10.8)=9.11
S甲=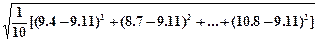 =1.3
=1.3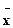 乙=
乙=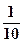 ×(9.1+8.7+7.1+9.8+9.7+8.5+10.1+9.2+10.1+9.1)=9.11=9.14
×(9.1+8.7+7.1+9.8+9.7+8.5+10.1+9.2+10.1+9.1)=9.11=9.14
S乙=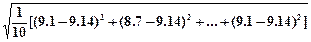 =0.9
=0.9
因为S甲>S乙,这说明了甲运动员的波动大于乙运动员的波动,
所以我们估计,乙运动员比较稳定。 12分
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案(本小题满分12分)某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如右图所示.
(1)下表是年龄的频数分布表,求正整数 的值;
的值;
| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 |  | 150 |  |
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
本小题满分12分)
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组 ,第二组
,第二组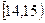 ……第五组
……第五组 ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.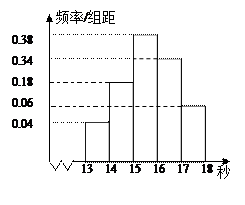
(Ⅰ)求这组数据的众数和中位数(精确到0.1);
(II)设 表示样本中两个学生的百米测
表示样本中两个学生的百米测
试成绩,已知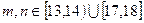
求事件“ ”的概率.
”的概率.
(Ⅲ) 根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如下 表
表
| 性别 是否达标 | 男 | 女 | 合计 |
| 达标 | 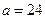 | 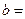 ______ ______ | _____ |
| 不达标 | 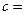 _____ _____ | 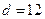 | _____ |
| 合计 | ______ | ______ |  |
、某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天100颗种子的发芽数,如下
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差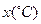 | 10 | 11 | 13 | 12 | 8 |
发芽数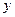 颗 颗 | 23 | 25 | 30 | 26 | 16 |
 求线性回归方程,再用被选取点2组数据进行检验
求线性回归方程,再用被选取点2组数据进行检验(1)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求
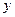 关于
关于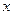 的线性回归方程
的线性回归方程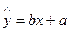 ;
;(2)若线性回归方程得到的估计数据与所选点检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得到的线性回归方程是否可靠?
参考公式:
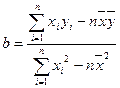 ,
,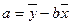
(13分)
某研究机构为了研究人的脚的大小(码)与身高(厘米)之间的关系,随机抽测了20人,得到如下数据:
| 序号 | 身高x | 脚长y | 序号 | 身高x | 脚长y |
| 1 | 176 | 42 | 11 | 179 | 44 |
| 2 | 175 | 44 | 12 | 169 | 43 |
| 3 | 174 | 41 | 13 | 185 | 45 |
| 4 | 180 | 44 | 14 | 166 | 40 |
| 5 | 170 | 42 | 15 | 174 | 42 |
| 6 | 178 | 43 | 16 | 167 | 42 |
| 7 | 173 | 42 | 17 | 173 | 41 |
| 8 | 168 | 40 | 18 | 174 | 42 |
| 9 | 190 | 46 | 19 | 172 | 42 |
| 10 | 171 | 42 | 20 | 175 | 41 |
(1)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”,“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”.请根据上表数据完成如下2×2列联表;
| | 高个 | 非高个 | 合计 |
| 大脚 | | | |
| 非大脚 | | 12 | |
| 合计 | | | 20 |
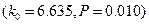
17.有甲乙两个班级进行数学考 试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10[来源:学科网ZXXK] | | |
| 乙班 | | 30 | [来源:学#科#网] |
| 合计 | | | 105 |
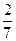
(1)请完成上面的列联表;
(2)根据列联表的数据,若按95%的可靠性要求,能否认为“成
 绩与班级有关系”。
绩与班级有关系”。(3)若按下面的方法从甲班优秀的学生抽取一人;把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取的人的序号,试求抽到6或10的概率。

 级的
级的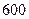 名学生参加一次科普知识竞赛,然后随机抽取
名学生参加一次科普知识竞赛,然后随机抽取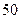 名学生的成绩进行统计分析.
名学生的成绩进行统计分析.