题目内容
(本小题满分12分)某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如右图所示.
(1)下表是年龄的频数分布表,求正整数 的值;
的值;
| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 |  | 150 |  |
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
(1) 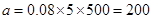 ,
, 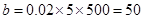 .
.
(2)第1,2,3组分别抽取1人,1人,4人.
(3)至少有1人年龄在第3组的概率为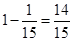 .
.
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
通过市场调查,得到某产品的资金投入x(万元)与获得的利润y(万元)的数据,如表所示:
| 资金投入x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 6 | 9 |
(Ⅱ)根据上表提供的数据,用最小二乘法求线性回归直线方程=x+;
(Ⅲ)现投入资金10万元,估计获得的利润为多少万元?
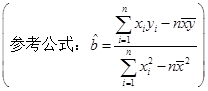
(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量( 吨)与相应的生产能耗
吨)与相应的生产能耗 (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
 | 3 | 4 | 5 | 6 |
 | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;并指出x,y 是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出
 关于
关于 的线性回归方程
的线性回归方程 ;
;(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式
 ,
, )
) (本小题满分12分)某种产品的广告费支出 与销售额
与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
(2)请根据上表提供的数据,用最小二乘法求出
 关于
关于 的线性回归方程
的线性回归方程 .(其中
.(其中 )
) (本小题12分)甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5项预赛成绩记录如下:
| 甲 | 82 | 82 | 79 | 95 | 87 |
| 乙 | 95 | 75 | 80 | 90 | 85 |
(2)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.


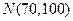 。已知成绩在90分以上(含90分)的学生有12名。
。已知成绩在90分以上(含90分)的学生有12名。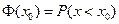
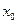
 次运动会甲、乙两名射击运动员成绩如下:
次运动会甲、乙两名射击运动员成绩如下:
 5,1
5,1 0.1,9.2,10.1,9.1;
0.1,9.2,10.1,9.1;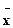 和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定。
和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定。