题目内容
【题目】如图，在四棱锥
中，平面
平面
，底面是边长为2的正方形，且
，
.
（Ⅰ）证明：
；
（Ⅱ）求平面
与平面
所成二面角的正弦值.
【答案】（Ⅰ）见解析 （Ⅱ）
【解析】
（1）面面垂直只需证明线面垂直即证：
（2）建立空间直角坐标系，利用平面
与面
的法向量所成的夹角公式即可求出平面与平面
（Ⅰ）
证明：（1）因为平面
面
，平面
平面
，
,
平面
,所以
平面
又
平面，所以
又
，
，所以
面
又
面
，所以平面
平面
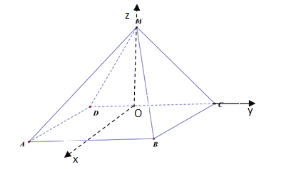
（2）取DC的中点O，连接MO，由DM＝MC得MO⊥DC。
又MO⊥BC，所以MO⊥平面ABCD，如图建立空间直角坐标系
则M（0，0，1），A（2，-1，0），B（2，1，0）
,
.
设
是平面MAB的一个法向量
则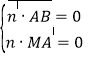
即
可取
，
是平面MCD的一个法向量
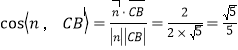
平面MAB与平面MCD所成二面角的正弦值是
练习册系列答案
相关题目
【题目】
年
月
日“世界读书日”来临之际，某校为了了解中学生课外阅读情况，随机抽取了
名学生，并获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表.
组号 | 分组 | 频数 | 频率 |
1 | [0，5） | 5 | 0.05 |
2 | [5，10） | a | 0.35 |
3 | [10，15） | 30 | b |
4 | [15，20） | 20 | 0.20 |
5 | [20，25] | 10 | 0.10 |
合计 | 100 | 1 | |
（1）求
、
的值
（2）作出这些数据的频率分布直方图
（3）假设每组数据组间是平均分布的，试估计该组数据的平均数和中位数.（同一组中的数据用该组区间的中点值作代表）
