题目内容
【题目】如图，多面体ABCD﹣A1B1C1D1为正方体，则下面结论正确的是（ ）
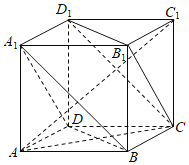
A.A1B∥B1C
B.平面CB1D1⊥平面A1B1C1D1
C.平面CB1D1∥平面A1BD
D.异面直线AD与CB1所成的角为30°
【答案】C
【解析】
根据正方体的顶点位置，可判断A1B、B1C是异面直线；平面CB1D1内不存在与平面A1B1C1D1
垂直的直线，平面A1B1C1D1内不存在直线垂直平面CB1D1，平面CB1D1不垂直平面A1B1C1D1；根据面面平行的判断定理可证平面CB1D1∥平面A1BD；根据正方体边的平行关系，可得异面直线AD与CB1所成的角为45°，即可得出结论.
选项A:
平面
平面
平面
，
是异面直线，该选项不正确；
选项B:由正方体可知
，
平面
，
平面
，
同理
平面
，
而平面
内不存在与
平行的直线，
所以平面内不存在直线垂直平面CB1D1；
同理平面CB1D1内不存在垂直平面A1B1C1D1的直线，
所以平面CB1D1不垂直平面A1B1C1D1，故该选项不正确；
选项C：由正方体可得
，可证
平面，
同理可证
平面，根据面面平行的判断定理
可得平面CB1D1∥平面A1BD，故该选项正确；
选项D: 
，异面直线AD与CB1所成的角为
而
，故该选项不正确.
故选:C
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案【题目】为了鼓励大家节约用水，自2013年以后，上海市实行了阶梯水价制度，其中每户的综合用水单价与户年用水量的关系如下表所示．
分档 | 户年用水量 | 综合用水单价/（元· |
第一阶梯 | 0 | 3.45 |
第二阶梯 | 220 | 4.83 |
第三阶梯 | 300以上 | 5.83 |
记户年用水量为
时应缴纳的水费为
元．
（1）写出的解析式；
（2）假设居住在上海的张明一家2015年共用水
，则张明一家2015年应缴纳水费多少元？
【题目】近几年来，“精准扶贫”是政府的重点工作之一，某地政府对240户贫困家庭给予政府资金扶助，以发展个体经济，提高家庭的生活水平.几年后，一机构对这些贫困家庭进行回访调查，得到政府扶贫资金数、扶贫贫困家庭数
（户）与扶贫后脱贫家庭数
（户）的数据关系如下：
政府扶贫资金数（万元） | 3 | 5 | 7 | 9 |
政府扶贫贫困家庭数 | 20 | 40 | 80 | 100 |
扶贫后脱贫家庭数 | 10 | 30 | 70 | 90 |
(Ⅰ)求几年来该地依靠“精准扶贫”政策的脱贫率是多少；（答案精准到0.1%）
(Ⅱ)从政府扶贫资金数为3万元和7万元并且扶贫后脱贫的家庭中按分层抽样抽取8户，再从这8户中随机抽取两户家庭，求这两户家庭的政府扶贫资金总和为10万元的概率.
