题目内容
3. 正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且$EF=\frac{{\sqrt{2}}}{2}$,则三棱锥B-AEF的体积为是$\frac{1}{12}$.
正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且$EF=\frac{{\sqrt{2}}}{2}$,则三棱锥B-AEF的体积为是$\frac{1}{12}$.
分析 计算三角形BEF的面积和A到平面BEF的距离,即可求出所求几何体的体积.
解答 解:∵B1D1∥平面ABCD,又E、F在直线D1B1上运动,
∴EF∥平面ABCD.
∴点B到直线B1D1的距离不变,故△BEF的面积为$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$×1=$\frac{\sqrt{2}}{4}$.
∵点A到平面BEF的距离为$\frac{\sqrt{2}}{2}$,
∴VA-BEF=$\frac{1}{3}$×$\frac{\sqrt{2}}{4}$×$\frac{\sqrt{2}}{2}$=$\frac{1}{12}$.
故答案为:$\frac{1}{12}$.
点评 本题考查几何体的体积的求法,考查计算能力,解题时要认真审题,注意体积中的不变量.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
13.把二进制数1101(2)化为十进制数是( )
| A. | 26 | B. | 25 | C. | 13 | D. | 5 |
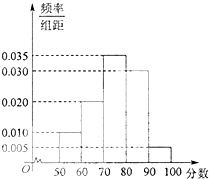 在一次区域统考中,为了解各学科的成绩情况,从所有考生成绩中随机抽出20位考生的成绩进行统计分析,其中数学学科的频率分布直方图如图所示,据此估计,在本次考试中数学成绩的方差为110.(同一组中的数据用该组区间的中点值作代表.
在一次区域统考中,为了解各学科的成绩情况,从所有考生成绩中随机抽出20位考生的成绩进行统计分析,其中数学学科的频率分布直方图如图所示,据此估计,在本次考试中数学成绩的方差为110.(同一组中的数据用该组区间的中点值作代表.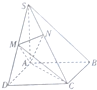 如图,四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.