题目内容
14. 在一次区域统考中,为了解各学科的成绩情况,从所有考生成绩中随机抽出20位考生的成绩进行统计分析,其中数学学科的频率分布直方图如图所示,据此估计,在本次考试中数学成绩的方差为110.(同一组中的数据用该组区间的中点值作代表.
在一次区域统考中,为了解各学科的成绩情况,从所有考生成绩中随机抽出20位考生的成绩进行统计分析,其中数学学科的频率分布直方图如图所示,据此估计,在本次考试中数学成绩的方差为110.(同一组中的数据用该组区间的中点值作代表.
分析 根据频率分布直方图,计算这组数据的平均数与方差即可.
解答 解:根据频率分布直方图,得;
该组数据的平均数是
$\overline{x}$=55×0.010×10+65×0.020×10+75×0.035×10+85×0.030×10+95×0.005×10=75;
方差是
s2=(75-55)2×0.1+(75-65)2×0.2+(75-75)2×0.35+(75-85)2×0.3+(75-95)2×0.05=110.
故答案为:110.
点评 本题考查了利用频率分布直方图求数据的平均数与方差的应用问题,是基础题目.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
5.某程序框图如图所示,若输出的S=41,则判断框内应填( )


| A. | k>4? | B. | k>5? | C. | k>6? | D. | k>7? |
4.若sin3θ-3$\sqrt{3}$cos3θ≥0,0<θ<2π,则角θ的取值范围是( )
| A. | [0,$\frac{π}{3}$] | B. | [$\frac{π}{3},π$] | C. | [$\frac{π}{3},\frac{4π}{3}$] | D. | [$\frac{π}{3},\frac{2π}{3}$] |
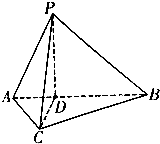 如图所示,三棱锥P-ABC中,点D为线段AB上一点,AC⊥BC,PD⊥平面ABC,AD=$\frac{1}{2}$DB,PD=BD,∠ABC=30°.
如图所示,三棱锥P-ABC中,点D为线段AB上一点,AC⊥BC,PD⊥平面ABC,AD=$\frac{1}{2}$DB,PD=BD,∠ABC=30°. 如图所示,已知D、E、F分别是△ABC的边BC、CA、AB的中点,P是△ABC内任意一点,求证:$\overrightarrow{PD}$+$\overrightarrow{PE}$+$\overrightarrow{PF}$=$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$.
如图所示,已知D、E、F分别是△ABC的边BC、CA、AB的中点,P是△ABC内任意一点,求证:$\overrightarrow{PD}$+$\overrightarrow{PE}$+$\overrightarrow{PF}$=$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$. 正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且$EF=\frac{{\sqrt{2}}}{2}$,则三棱锥B-AEF的体积为是$\frac{1}{12}$.
正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且$EF=\frac{{\sqrt{2}}}{2}$,则三棱锥B-AEF的体积为是$\frac{1}{12}$.