题目内容
13.函数y=Asin(ωx+φ)(0<φ<π)在一个周期内的图象如图,此函数的解析式为y=2sin(2x+$\frac{2π}{3}$)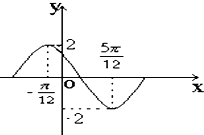
分析 根据所给的图象,可以看出图象的振幅是2,得到A=2,看出半个周期的值,得到ω,根据函数的图象过定点,把点的坐标代入求出φ的值,得到三角函数的解析式.
解答 解:由图象可知A=2,$\frac{T}{2}$=$\frac{5π}{12}$-(-$\frac{π}{12}$)=$\frac{π}{2}$,
∴T=π,
∴ω=2,
∴三角函数的解析式是y=2sin(2x+φ)
∵函数的图象过(-$\frac{π}{12}$,2)这一点,
把点的坐标代入三角函数的解析式,
∴2=2sin[2(-$\frac{π}{12}$)+φ]
∴φ-$\frac{π}{6}$=2kπ+$\frac{π}{2}$,
∵0<φ<π,
∴φ=$\frac{2π}{3}$,
∴三角函数的解析式是y=2sin(2x+$\frac{2π}{3}$)
故答案为:y=2sin(2x+$\frac{2π}{3}$)
点评 题考查三角函数的解析式的求法,本题解题的关键是求出φ的值,一般利用代入图象经过的一个点的坐标,代入的点一般是最高点或最低点,本题是一个中档题目.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
4.数列的通项公式是an=4n-1,则a6等于( )
| A. | 21 | B. | 22 | C. | 23 | D. | 24 |
1.对于任意实数x,代数式$\frac{1}{2}{x^2}$-3x+5的值是一个( )
| A. | 非负数 | B. | 正数 | C. | 负数 | D. | 整数 |
8.若函数f(x)=|x-a|+|x+1|,方程f(x)=$\sqrt{1-{x}^{2}}$有解时,a的取值范围为( )
| A. | [-2,0] | B. | [-$\sqrt{2},0$] | C. | [-$\sqrt{5}$,1] | D. | [1-$\sqrt{5}$,0] |
