题目内容
【题目】已知函数f(x)=ln(x+1),g(x)=kx(k∈R).
(1)证明:当x>0时,f(x)<x;
(2)证明:当k<1时,存在x0>0,使得对任意的x∈(0,x0),恒有f(x)>g(x).
【答案】
(1)解:令F(x)=f(x)﹣x=ln(1+x)﹣x,x∈(0,+∞),
则有F′(x)= ![]() ﹣1=﹣
﹣1=﹣ ![]() .
.
当x∈(0,+∞)时,F′(x)<0,所以F(x)在(0,+∞)上单调递减;
故当x>0时,F(x)<F(0)=0,即当x>0时,f(x)<x
(2)解:令G(x)=f(x)﹣g(x)=ln(1+x)﹣kx,x∈(0,+∞),
则有G′(x)= ![]() ﹣k=
﹣k= ![]() .
.
当k≤0时G′(x)>0,所以G(x)在(0,+∞)上单调递增,
G(x)>G(0)=0,故对任意正实数x0均满足题意.
当0<k<1时,令G′(x)=0,得x= ![]() =
= ![]() ﹣1>0.
﹣1>0.
取x0= ![]() ﹣1,对任意x∈(0,x0),恒有G′(x)>0,
﹣1,对任意x∈(0,x0),恒有G′(x)>0,
从而G(x)在(0,x0)上单调递增,G(x)>G(0)=0,即f(x)>g(x)
【解析】(1)构造函数F(x)=f(x)﹣x=ln(1+x)﹣x,x∈(0,+∞),利用函数F(x)的单调性,只需求出F(x)值域即可;(2)构造函数G(x)=f(x)﹣g(x)=ln(1+x)﹣kx,x∈(0,+∞),利用其单调性,讨论其值域情况即可.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.

【题目】观察研究某种植物的生长速度与温度的关系,经过统计,得到生长速度(单位:毫米/月)与月平均气温的对比表如下:
温度 | -5 | 0 | 6 | 8 | 12 | 15 | 20 |
生长速度 | 2 | 4 | 5 | 6 | 7 | 8 | 10 |
(1)求生长速度![]() 关于温度
关于温度![]() 的线性回归方程;(斜率和截距均保留为三位有效数字);
的线性回归方程;(斜率和截距均保留为三位有效数字);
(2)利用(1)中的线性回归方程,分析气温从![]() 至
至![]() 时生长速度的变化情况,如果某月的平均气温是
时生长速度的变化情况,如果某月的平均气温是![]() 时,预测这月大约能生长多少.
时,预测这月大约能生长多少.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
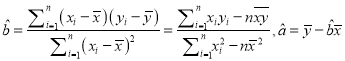 .
.