题目内容
设f(x)=x2–2ax+2,当x∈[–1,+∞)时,f(x)>a恒成立,求a的取值范围

a∈(–3,1
解法一:由f(x)>a,在[–1,+∞)上恒成立
 x2–2ax+2–a>0在[–1,+∞)上恒成立.
x2–2ax+2–a>0在[–1,+∞)上恒成立.
考查函数g(x)=x2–2ax+2–a的图像在[–1,+∞]时位于x轴上方. 如图两种情况:
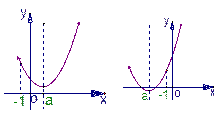
不等式的成立条件是:
(1)Δ=4a2–4(2–a)<0 a∈(–2,1)
a∈(–2,1)
(2)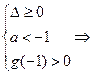 a∈(–3,–2
a∈(–3,–2 ,
,
综上所述a∈(–3,1).
解法二:由f(x)>a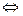 x2+2>a(2x+1)
x2+2>a(2x+1)
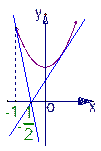
令y1=x2+2,y2=a(2x+1),在同一坐标系中作出两个函数的图像.
如图满足条件的直线l位于l1与l2之间,而直线l1、l2对应的a值(即直线的斜率)分别为1,–3,故直线l对应的a∈(–3,1).
 x2–2ax+2–a>0在[–1,+∞)上恒成立.
x2–2ax+2–a>0在[–1,+∞)上恒成立.考查函数g(x)=x2–2ax+2–a的图像在[–1,+∞]时位于x轴上方. 如图两种情况:

不等式的成立条件是:
(1)Δ=4a2–4(2–a)<0
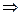 a∈(–2,1)
a∈(–2,1)(2)
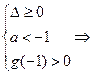 a∈(–3,–2
a∈(–3,–2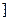 ,
,综上所述a∈(–3,1).
解法二:由f(x)>a
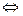 x2+2>a(2x+1)
x2+2>a(2x+1)令y1=x2+2,y2=a(2x+1),在同一坐标系中作出两个函数的图像.
如图满足条件的直线l位于l1与l2之间,而直线l1、l2对应的a值(即直线的斜率)分别为1,–3,故直线l对应的a∈(–3,1).


练习册系列答案
相关题目
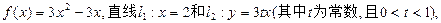
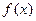 的图象以及直线l1、l2与函数
的图象以及直线l1、l2与函数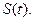
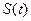 的解析式;
的解析式;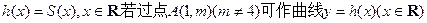 的三条切线,求实数m的取值范围。
的三条切线,求实数m的取值范围。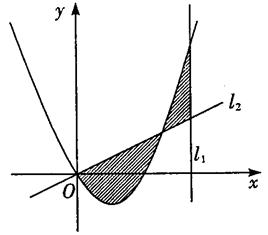
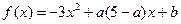
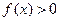 的解集为
的解集为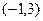 时,求实数
时,求实数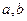 的值;
的值; 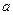 ,
,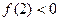 恒成立,求实数
恒成立,求实数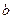 的取值范围;
的取值范围;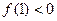 .
.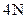 的物体时,长20 cm.在弹性限度内,所挂物体的重量每增加
的物体时,长20 cm.在弹性限度内,所挂物体的重量每增加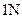 ,弹簧就伸长
,弹簧就伸长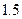 cm.试写出弹簧的长度
cm.试写出弹簧的长度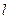 (cm)与所挂物体重量
(cm)与所挂物体重量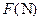 之间的关系的方程.
之间的关系的方程.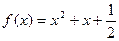 的定义域是
的定义域是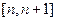 (
(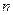 是正整数),那么
是正整数),那么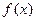 的值域中共有 个整数
的值域中共有 个整数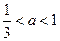 ,若
,若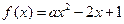 在区间
在区间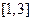 上的最大值为
上的最大值为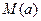 ,最小值为
,最小值为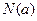 ,记
,记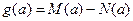 .
.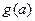 的解析表达式; (2)若对一切
的解析表达式; (2)若对一切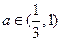 都有
都有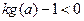 成立,求实数
成立,求实数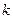 的取值范围.
的取值范围.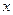 的不等式
的不等式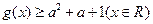 的解集为空集,则实数
的解集为空集,则实数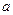 的取值范围是 .
的取值范围是 .  取3.1)?
取3.1)?