题目内容
已知二次函数f(x)是定义在R上的偶函数,且关于x的不等式f(x)<4x的解集为{x|1<x<3}.
(Ⅰ)求f(x)的解析式;
(Ⅱ)设F(x)=f(x)+bx,且当x∈[-1,2]时,函数F(x)的最小值为1,求实数b的值.
(Ⅰ)求f(x)的解析式;
(Ⅱ)设F(x)=f(x)+bx,且当x∈[-1,2]时,函数F(x)的最小值为1,求实数b的值.
(I)设f(x)=ax2+bx+c(a≠0),由f(x)是偶函数知f(x)的图象关于y轴对称,
则-
=0,即b=0,故f(x)=ax2+c.…(1分)
∵不等式f(x)<4x的解集为{x|1<x<3},
∴a>0且x1=1,x2=3是方程f(x)-4x=0即ax2-4x+c=0的两根.
由韦达定理,得
,
解得:a=1,c=3.…(5分)
∴f(x)=x2+3.…(6分)
(II)由( I)知,F(x)=x2+bx+3=(x+
)2+3-
,对称轴x=-
.…(7分)
下面分类讨论:
①当-
≥2,即b≤-4时,F(x)在[-1,2]上为减函数,
∴F(x)min=F(2)=2b+7=1,得b=-3(舍去).…(9分)
②当-
∈(-1,2),即-4<b<2时,F(x)min=F(-
)=-
+3=1,
∴b=-2
或b=2
(舍去).…(11分)
③当-
≤-1,即b≥2时,F(x)在[-1,2]上为增函数,
∴F(x)min=F(-1)=4-b=1,得b=3.…(13分)
综上所述,b=-2
或b=3为所求.…(14分)
则-
| b |
| 2a |
∵不等式f(x)<4x的解集为{x|1<x<3},
∴a>0且x1=1,x2=3是方程f(x)-4x=0即ax2-4x+c=0的两根.
由韦达定理,得
|
解得:a=1,c=3.…(5分)
∴f(x)=x2+3.…(6分)
(II)由( I)知,F(x)=x2+bx+3=(x+
| b |
| 2 |
| b2 |
| 4 |
| b |
| 2 |
下面分类讨论:
①当-
| b |
| 2 |
∴F(x)min=F(2)=2b+7=1,得b=-3(舍去).…(9分)
②当-
| b |
| 2 |
| b |
| 2 |
| b2 |
| 4 |
∴b=-2
| 2 |
| 2 |
③当-
| b |
| 2 |
∴F(x)min=F(-1)=4-b=1,得b=3.…(13分)
综上所述,b=-2
| 2 |

练习册系列答案
相关题目
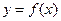 的图象经过三点
的图象经过三点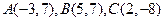 。
。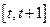 上的最大值和最小值。
上的最大值和最小值。