题目内容
7. 如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,EA=ED,AE⊥平面CDE.
如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,EA=ED,AE⊥平面CDE.(1)求证:AB⊥平面ADE;
(2)设M是线段BE上一点,当直线AM与平面EAD所成角的正弦值为$\frac{{2\sqrt{2}}}{3}$时,试确定点M的位置.
分析 (1)证明AE⊥CD,推出CD⊥平面ADE.利用直线与平面垂直的判定定理证明AB⊥平面ADE.
(2)由取AD中点O,取BC中点F,连接EO、OF.以OA、OF、OE分别为x、y、z轴建立如图所示的空间直角坐标系,设AB=2,推出$\overrightarrow{AM}$,设AM与平面EAD所成角为θ,利用平面EAD的一法向量,直线AM与平面EAD所成角的正弦值为$\frac{{2\sqrt{2}}}{3}$,求解即可.
解答 (1)证明:∵AE⊥平面CDE,CD?平面CDE,
∴AE⊥CD.(2分)
在正方形ABCD中,CD⊥AD,
∵AD∩AE=A,∴CD⊥平面ADE.
∵AB∥CD,∴AB⊥平面ADE.(4分)
(2)解:由(1)得平面EAD⊥平面ABCD,取AD中点O,取BC中点F,连接EO、OF.
∵EA=ED,∴EO⊥AD,
∴EO⊥平面ABCD.(5分)
以OA、OF、OE分别为x、y、z轴建立如图所示的空间直角坐标系,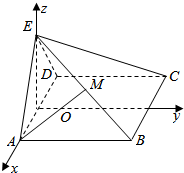
不妨设AB=2,则A(1,0,0),B(1,2,0),E(0,0,1).(6分)
设M(x,y,z).
∴$\overrightarrow{BM}$=(x-1,y-2,z),$\overrightarrow{BE}$=(-1,-2,1)
∵B,M,E三点共线,设$\overrightarrow{BM}$=λ$\overrightarrow{BE}$,
∴M(1-λ,2-2λ,λ),
∴$\overrightarrow{AM}$=(-λ,2-2λ,λ).(8分)
设AM与平面EAD所成角为θ,∵平面EAD的一法向量为$\overrightarrow{n}$=(0,1,0),(9分)
∴sinθ=$\left|\frac{\overrightarrow{AM}•\overrightarrow{n}}{\left|\overrightarrow{AM}\right|\left|\overrightarrow{n}\right|}\right|$,∵直线AM与平面EAD所成角的正弦值为$\frac{{2\sqrt{2}}}{3}$,
可得:$\frac{|2-2λ|}{\sqrt{2{λ}^{2}+{(2-2λ)}^{2}}}=\frac{2\sqrt{2}}{3}$,
解得λ=$\frac{1}{3}$或λ=-1(舍去),(11分)
∴点M为线段BE上靠近B的三等分点.(12分)
点评 本题考查直线与平面垂直,直线与平面所成角的求法,考查空间想象能力以及计算能力.

| A. | (-∞,-$\frac{24}{7}$) | B. | (0,$\frac{24}{7}$) | C. | (-$\frac{24}{7}$,0) | D. | (-$\frac{24}{7}$,$\frac{24}{7}$) |
 如图,正方体ABCD-A1B1C1D1中,PQ是异面直线A1D与AC的公垂线,则直线PQ与BD1的位置关系为( )
如图,正方体ABCD-A1B1C1D1中,PQ是异面直线A1D与AC的公垂线,则直线PQ与BD1的位置关系为( )| A. | 平行 | B. | 异面 | C. | 相交 | D. | 无法判断 |

 如图,在四面体ABCD中,平面BAD⊥平面CAD,∠BAD=90°.M,N,Q分别为棱AD,BD,AC的中点.
如图,在四面体ABCD中,平面BAD⊥平面CAD,∠BAD=90°.M,N,Q分别为棱AD,BD,AC的中点. 如图,正方体ABCD-A1B1C1D1中,E,F分别是AB,BC的中点.求证:
如图,正方体ABCD-A1B1C1D1中,E,F分别是AB,BC的中点.求证: