题目内容
19．不等式组$\left\{\begin{array}{l}{x+y≤4}\\{3x-y≥0}\\{y≥0}\end{array}\right.$的解集记为D，下面四个命题：①?（x，y）∈D，2x-y≤10；②?（x，y）∈D，2x-y≥-2；③?（x，y）∈D，2x-y＜0；④?（x，y）∈D，2x-y=9．
其中，正确命题的个数为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据题意，画出不等式组$\left\{\begin{array}{l}{x+y≤4}\\{3x-y≥0}\\{y≥0}\end{array}\right.$表示的平面区域D，结合图形进行解答即可．
解答 解：∵不等式组$\left\{\begin{array}{l}{x+y≤4}\\{3x-y≥0}\\{y≥0}\end{array}\right.$表示的平面区域D为阴影区域△OAC：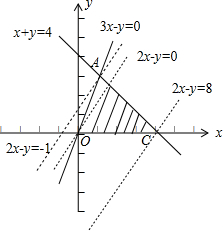
在阴影区域△OAC中，
对于①，?（x，y）∈D，2x-y≤8，∴2x-y≤10成立，①正确；
对于②，∵2x-y≥-1，∴不?（x，y）∈D，使2x-y＜-2，∴②错误；
对于③，?（x，y）∈D，2x-y＜7，∴③正确；
对于④，?（x，y）∈D，使2x-y≤5，∴④正确；
综上，正确命题的个数是3．
故选：C．
点评 本题考查了线性规划的应用问题，解题时应作出平面区域，结合图形解答问题，是基础题目．
练习册系列答案
相关题目
如图，在底面为菱形ABCD的四棱柱ABCD-A1B1C1D1中，∠ABC=60°，AA1=AB=2，A1B=A1D=2$\sqrt{2}$．
如图，正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD，EA=ED，AE⊥平面CDE．
11．设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（b≥$\frac{\sqrt{3}}{2}$a＞0）右焦点为F（c，0）（c＞0），方程ax2+bx-c=0的两实根分别为x1，x2，则x12+x22的取值范围是（ ）
| A． | （0，$\frac{3}{2}$] | B． | （1，$\frac{3}{2}$] | C． | （1，$\frac{3}{4}$] | D． | （1，$\frac{7}{4}$] |
如图正四棱锥S-ABCD，底面边长为2，P为侧棱SD上靠近D的三等分点，