题目内容
若函数f(x)=|ax+x2-xlna-t|-1(0<a<1)有零点,则实数t的最小值是______.
f(x)有零点?不等式ax+x2-xlna-t≤1有实数解?t≥ax+x2-xlna-1有实数解?t≥(ax+x2-xlna-1)min,
令g(x)=ax+x2-xlna-1,则g′(x)=axlna+2x-lna,g″(x)=axln2a+2>0,
∴g′(x)为增函数,
而g′(0)=a0lna+2×0-lna=0,
∴x>0时,g′(x)>g′(0)=0,g(x)为增函数;
当x<0时,g′(x)<g′(0)=0,g(x)为减函数;
∴g(x)min=g(0)=0,
∴t≥0,即实数t的最小值为0.
故答案为:0.
令g(x)=ax+x2-xlna-1,则g′(x)=axlna+2x-lna,g″(x)=axln2a+2>0,
∴g′(x)为增函数,
而g′(0)=a0lna+2×0-lna=0,
∴x>0时,g′(x)>g′(0)=0,g(x)为增函数;
当x<0时,g′(x)<g′(0)=0,g(x)为减函数;
∴g(x)min=g(0)=0,
∴t≥0,即实数t的最小值为0.
故答案为:0.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
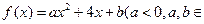 R),设关于
R),设关于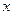 的方程
的方程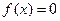 的两实根为
的两实根为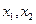 ,方程
,方程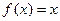 的两实根为
的两实根为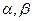 .(Ⅰ)若
.(Ⅰ)若 ,求
,求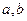 的关系式;(Ⅱ)若
的关系式;(Ⅱ)若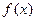 的解析式; (Ⅲ)若
的解析式; (Ⅲ)若 .
. 唯一的一个零点同时在区间
唯一的一个零点同时在区间 、
、 、
、 、
、 内,
内, 内有零点
内有零点 内有零点
内有零点 内无零点
内无零点 内无零点
内无零点