题目内容
已知函数y=mx的图象与函数y=
的图象没有公共点,则实数m的取值范围______.
| |x|-1 |
| |x-1| |
由y=
=
.
图象如图,
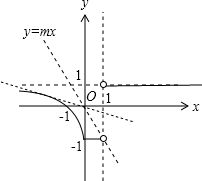
由
,得mx2-(m+1)x-1=0.
当m≠0时,由△=[-(m+1)]2+4m=0,解得m=-3-2
(舍),或m=-3+2
.
由数形结合可知,
满足函数y=mx的图象与函数y=
的图象没有公共点的实数m的取值范围是-1≤m<-3+2
.
故答案为-1≤m<-3+2
.
| |x|-1 |
| |x-1| |
|
图象如图,

由
|
当m≠0时,由△=[-(m+1)]2+4m=0,解得m=-3-2
| 2 |
| 2 |
由数形结合可知,
满足函数y=mx的图象与函数y=
| |x|-1 |
| |x-1| |
| 2 |
故答案为-1≤m<-3+2
| 2 |

练习册系列答案
相关题目
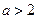 ,则函数
,则函数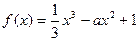 在区间
在区间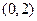 上恰好有 ( )
上恰好有 ( )