题目内容
7.已知函数f(x)=msin2x+cos2x的图象过点($\frac{π}{12},\sqrt{3}$).(Ⅰ)求m的值;
(Ⅱ)将函数y=f(x)的图象向右平移$\frac{π}{6}$个单位得到y=g(x)的图象,求y=g(x)在区间[0,$\frac{π}{2}$]上的最大值和最小值.
分析 (Ⅰ)根据点和函数的关系,代入即可求m的值;
(Ⅱ)根据函数平移关系求出g(x)的图象,结合三角函数的单调性和最值之间的关系进行求解即可.
解答 解:(Ⅰ)∵f(x)=msin2x+cos2x的图象过点($\frac{π}{12},\sqrt{3}$).
∴f($\frac{π}{12}$)=msin$\frac{π}{6}$+cos$\frac{π}{6}$=$\sqrt{3}$,
即$\frac{1}{2}$m+$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
解得m=$\sqrt{3}$;
(Ⅱ)∵m=$\sqrt{3}$;
∴f(x)=$\sqrt{3}$sin2x+cos2x=2sin(2x+$\frac{π}{6}$),
函数y=f(x)的图象向右平移$\frac{π}{6}$个单位得到y=g(x)的图象,
即g(x)=2sin[2(x-$\frac{π}{6}$)+$\frac{π}{6}$]=2sin(2x-$\frac{π}{6}$),
∵0≤x≤$\frac{π}{2}$,
∴-$\frac{π}{6}$≤2x-$\frac{π}{6}$≤$\frac{5π}{6}$,
即当2x-$\frac{π}{6}$=$\frac{π}{2}$,即x=$\frac{π}{3}$时,函数g(x)取得最大值g($\frac{π}{3}$)=2sin$\frac{π}{2}$=2,
当2x-$\frac{π}{6}$=-$\frac{π}{6}$,即x=0时,函数g(x)取得最小值g(-$\frac{π}{6}$)=2sin(-$\frac{π}{6}$)=-1,
即y=g(x)在区间[0,$\frac{π}{2}$]上的最大值和最小值分别为2,-1.
点评 本题主要考查三角函数单调性和最值的应用,根据三角函数的辅助角公式将函数进行化简是解决本题的关键.

| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
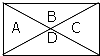 用5种不同的颜色给如图标有A,B,C,D的各部分涂色,每部分只涂一种颜色,且相邻两部分不同颜色,则不同的涂色方法共有( )
用5种不同的颜色给如图标有A,B,C,D的各部分涂色,每部分只涂一种颜色,且相邻两部分不同颜色,则不同的涂色方法共有( )| A. | 160种 | B. | 240种 | C. | 260种 | D. | 360种 |
| A. | C${\;}_{7}^{4}$ | B. | C${\;}_{8}^{4}$ | C. | C${\;}_{8}^{3}$ | D. | C${\;}_{9}^{3}$ |
| A. | f(x)=x3 | B. | f(x)=-|x+1| | C. | f(x)=ln$\frac{2-x}{2+x}$ | D. | f(x)=$\frac{{a}^{x}+{a}^{-x}}{2}$ |
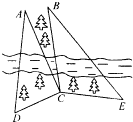 如图,为了开发某森林区,某测量人员身处这个森林区一条河的南岸,为了测量河对岸不能到达的两点A,B之间的距离,同时由于树木的遮挡,不可能分别在两个不同地点同时观察到点A,B;但她在南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;已知A,B,C,D,E在同一水平面内并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(km).
如图,为了开发某森林区,某测量人员身处这个森林区一条河的南岸,为了测量河对岸不能到达的两点A,B之间的距离,同时由于树木的遮挡,不可能分别在两个不同地点同时观察到点A,B;但她在南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;已知A,B,C,D,E在同一水平面内并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(km).