题目内容
17．已知函数f（x）=x3+ax在[1，+∞）上单调递增函数，则实数a的最小值是（ ）| A． | 0 | B． | -1 | C． | -2 | D． | -3 |
分析 先求函数的导函数f′（x），由函数f（x）=x3+ax在[1，+∞）上是增函数，知f′（x）≥0在[1，+∞）上恒成立，从而转化为求函数f′（x）在[1，+∞）上的最小值即可
解答 解：f′（x）=3x2+a．
∵函数f（x）=x3+ax在[1，+∞）上是增函数．
∴f′（x）=3x2+a≥0在[1，+∞）上恒成立．
∵f′（x）=3x2+a在[1，+∞）上增函数．
∴3x2+a≥3×12+a=3+a．
∴3+a≥0．
∴a≥-3．
实数a的最小值是：-3．
故选：D．
点评 本题考察了导数在函数单调性中的应用，不等式恒成立问题的解法，转化化归的思想方法．
练习册系列答案
相关题目
8．一个算法的程序框图所图所示，则该程序输出的结果为（ ）
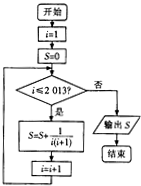
| A． | $\frac{2012}{2013}$ | B． | $\frac{2013}{2014}$ | C． | $\frac{1}{2013}$ | D． | $\frac{1}{2014}$ |
2．在数列{an}中，a1=2，an+1=1-$\frac{1}{{a}_{n}}$，则a2010=（ ）
| A． | 1 | B． | -1 | C． | $\frac{1}{2}$ | D． | 2 |