Question

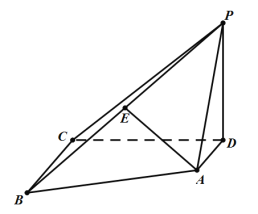
【题目】在直三棱柱中，是棱的中点.

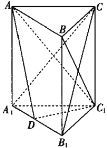
（1）证明：直线平面；

（2）若，，证明：平面平面.

Answer 1

【答案】（1）证明见解析（2）证明见解析

【解析】

（1）设与的交点为，连接，推导出，结合线面平行的判定定理，即可求解；

（2）推导出四边形为菱形，从而得到，证得平面，得到，再由，得出平面，进而结合面面垂直的判定定理，即可证得平面平面.

（1）设与的交点为，连接，如图所示，

在直三棱柱中，得侧面四边形是平行四边形，

∴点为的中点.

又∵是棱的中点，

在中，为中位线，可得.

而平面，平面，所以直线平面.

（2）∵侧面四边形是平行四边形，，

∴四边形为菱形，所以，

在直三棱柱中，得平面，

又因为平面，所以，

又由，平面，平面，，

所以平面，

又∵平面，所以，

又有，平面，平面，，

∴平面，

又∵平面，

∴平面平面.