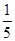题目内容
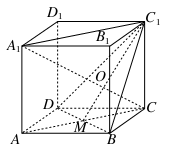
如图所示，正方体ABCD－A1B1C1D1中，A1C与截面DBC1交于O点，AC，BD交于M点，求证：C1，O，M三点共线．
见解析
证明：∵C1∈平面A1ACC1，且C1∈平面DBC1，
∴C1是平面A1ACC1与平面DBC1的公共点．
又∵M∈AC，∴M∈平面A1ACC1.
∵M∈BD，∴M∈平面DBC1，
∴M也是平面A1ACC1与平面DBC1的公共点，
∴C1M是平面A1ACC1与平面DBC1的交线．
∵O为 A1C与截面DBC1的交点，
∴O∈平面A1ACC1，O∈平面DBC1，
即O也是两平面的公共点，
∴O∈直线C1M，即C1，O，M三点共线．
∴C1是平面A1ACC1与平面DBC1的公共点．
又∵M∈AC，∴M∈平面A1ACC1.
∵M∈BD，∴M∈平面DBC1，
∴M也是平面A1ACC1与平面DBC1的公共点，
∴C1M是平面A1ACC1与平面DBC1的交线．
∵O为 A1C与截面DBC1的交点，
∴O∈平面A1ACC1，O∈平面DBC1，
即O也是两平面的公共点，
∴O∈直线C1M，即C1，O，M三点共线．
练习册系列答案
相关题目
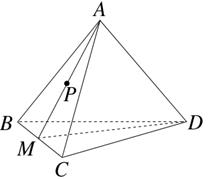
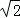，点E在侧棱AA1上，点F在侧棱BB1上，且AE=2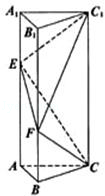
.
、
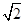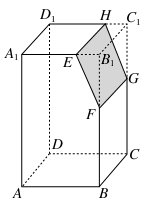
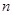是两条不同的直线，
、
是两个不同的平面，则（ ）
，
，则
，
，则
，
，
，则
