题目内容
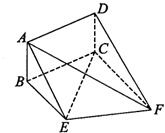
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=
CD,M是线段AE上的动点.
(Ⅰ)试确定点M的位置,使AC∥平面DMF,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值.

| 1 |
| 2 |
(Ⅰ)试确定点M的位置,使AC∥平面DMF,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值.

(Ⅰ)当M是线段AE的中点时,AC∥平面DMF.
证明如下:
连结CE,交DF于N,连结MN,
由于M、N分别是AE、CE的中点,所以MN∥AC,
由于MN?平面DMF,又AC不包含于平面DMF,
∴AC∥平面DMF.(4分)
(Ⅱ)方法一:过点D作平面DMF与平面ABCD的交线l,
∵AC∥平面DMF,∴AC∥l,
过点M作MG⊥AD于G,
∵平面ABCD⊥平面CDEF,DE⊥CD,
∴DE⊥平面ABCD,∴平面ADE⊥平面ABCD,
∴MG⊥平面ABCD,
过G作GH⊥l于H,连结MH,则直线l⊥平面MGH,∴l⊥MH,
∴∠MHG是平面MDF与平面ABCD所成锐二面角的平面角.(8分)
设AB=2,则DG=1,GH=DGsin∠GDH=DGsin∠DAC=1×
=
,MG=
DE=1,则MH=
=
,(11分)
∴cos∠MHG=
=
÷
=
,
∴所求二面角的余弦值为
.(12分)
方法二:∵平面ABCD⊥平面CDEF,DE⊥CD,
∴DE⊥平面ABCD,可知AD,CD,DE两两垂直,
分别以
,
,
的方向为x,y,z轴,
建立空间直角坐标系O-xyz.
设AB=2,则M(1,0,1),F(0,4,2),
=(1,0,1),
=(0,4,2),
设平面MDF的法向量n1=(x,y,z),
则
,∴
,
令y=1,得平面MDF的一个法向量
=(2,1,-2),(8分)
取平面ABCD的法向量
=(0,0,1),(9分)
由cos<
,
>=
=-
,(11分)
∴平面MDF与平面ABCD所成锐二面角的余弦值为
.(12分)
证明如下:
连结CE,交DF于N,连结MN,
由于M、N分别是AE、CE的中点,所以MN∥AC,

由于MN?平面DMF,又AC不包含于平面DMF,
∴AC∥平面DMF.(4分)
(Ⅱ)方法一:过点D作平面DMF与平面ABCD的交线l,
∵AC∥平面DMF,∴AC∥l,
过点M作MG⊥AD于G,
∵平面ABCD⊥平面CDEF,DE⊥CD,
∴DE⊥平面ABCD,∴平面ADE⊥平面ABCD,

∴MG⊥平面ABCD,
过G作GH⊥l于H,连结MH,则直线l⊥平面MGH,∴l⊥MH,
∴∠MHG是平面MDF与平面ABCD所成锐二面角的平面角.(8分)
设AB=2,则DG=1,GH=DGsin∠GDH=DGsin∠DAC=1×
| 2 | ||
|
| 2 | ||
|
| 1 |
| 2 |
(
|
| 3 | ||
|
∴cos∠MHG=
| GH |
| MH |
| 2 | ||
|
| 3 | ||
|
| 2 |
| 3 |
∴所求二面角的余弦值为
| 2 |
| 3 |
方法二:∵平面ABCD⊥平面CDEF,DE⊥CD,
∴DE⊥平面ABCD,可知AD,CD,DE两两垂直,
分别以
| DA |
| DC |
| DE |
建立空间直角坐标系O-xyz.
设AB=2,则M(1,0,1),F(0,4,2),
| DM |
| DF |
设平面MDF的法向量n1=(x,y,z),

则
|
|
令y=1,得平面MDF的一个法向量
| n |
取平面ABCD的法向量
| m |
由cos<
| n |
| m |
| -2 | ||
|
| 2 |
| 3 |
∴平面MDF与平面ABCD所成锐二面角的余弦值为
| 2 |
| 3 |

练习册系列答案
相关题目

 中,底面
中,底面 是矩形,
是矩形,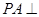 平面
平面 ,
, ,
, 依次是
依次是 的中点.
的中点.
 ;
;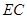 与平面
与平面 所成角的正弦值.
所成角的正弦值.