题目内容
(12分)(2011•湖北)如图,已知正三棱柱ABC﹣A1B1C1的底面边长为2,侧棱长为3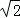 ,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2
,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2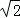 ,BF=
,BF=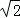 .
.
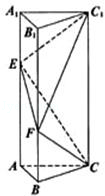
(I) 求证:CF⊥C1E;
(II) 求二面角E﹣CF﹣C1的大小.
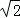 ,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2
,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2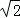 ,BF=
,BF=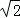 .
.
(I) 求证:CF⊥C1E;
(II) 求二面角E﹣CF﹣C1的大小.
(I)见解析(II)45°
试题分析:(I)欲证C1E⊥平面CEF,根据直线与平面垂直的判定定理可知只需证C1E与平面CEF内两相交直线垂直,根据勾股定理可知EF⊥C1E,C1E⊥CE,又EF∩CE=E,满足线面垂直的判定定理,最后根据线面垂直的性质可知CF⊥C1E;
(II)根据勾股定理可知CF⊥EF,根据线面垂直的判定定理可知CF⊥平面C1EF,而C1F?平面C1EF,则CF⊥C1F,从而∠EFC1即为二面角E﹣CF﹣C1的平面角,在△C1EF是等腰直角三角形,求出此角即可.
解:(I)由已知可得CC1=
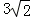 ,CE=C1F=
,CE=C1F=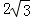 ,
,EF2=AB2+(AE﹣BF)2,EF=C1E=
 ,
,于是有EF2+C1E2=C1F2,CE2+C1E2=C1C2,
所以EF⊥C1E,C1E⊥CE.又EF∩CE=E,
所以C1E⊥平面CEF
由CF?平面CEF,故CF⊥C1E;
(II)在△CEF中,由(I)可得EF=CF=
 ,CE=
,CE=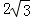 ,
,于是有EF2+CF2=CE2,所以CF⊥EF,
又由(I)知CF⊥C1E,且EF∩C1E=E,所以CF⊥平面C1EF
又C1F?平面C1EF,故CF⊥C1F
于是∠EFC1即为二面角E﹣CF﹣C1的平面角
由(I)知△C1EF是等腰直角三角形,所以∠EFC1=45°,即所求二面角E﹣CF﹣C1的大小为45°
点评:本题主要考查了空间直线与平面的位置关系和二面角的求法,同时考查了空间想象能力和推理论证的能力.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 中,底面
中,底面 是矩形,
是矩形,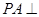 平面
平面 ,
, ,
, 依次是
依次是 的中点.
的中点.
 ;
;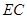 与平面
与平面 所成角的正弦值.
所成角的正弦值.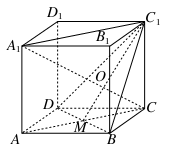
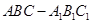 中,侧棱垂直于底面,
中,侧棱垂直于底面,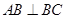 ,
,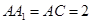 ,
,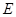 、
、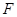 分别为
分别为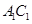 、
、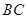 的中点.
的中点.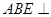 平面
平面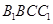 ;
;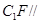 平面
平面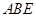 ;
; 的体积.
的体积.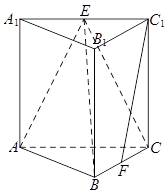
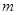 、
、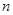 是两条直线,
是两条直线,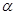 、
、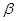 是两个平面,给出下列命题:①若
是两个平面,给出下列命题:①若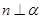 ,
,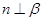 ,则
,则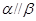 ;②若平面
;②若平面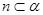 ,
,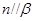 ,
,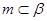 ,
,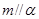 ,则
,则 个
个 个
个 个
个 个
个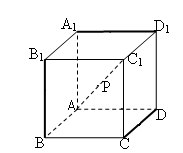
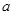 的正方形的四棱锥
的正方形的四棱锥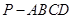 中,已知
中,已知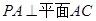 ,且
,且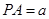 ,则直线
,则直线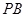 与平面
与平面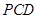 所成的角大小为 .
所成的角大小为 . 
 ,M,N分别是AC,BC的中点,则EM,AN所成角的余弦值等于________.
,M,N分别是AC,BC的中点,则EM,AN所成角的余弦值等于________.