题目内容
9.已知公差为d的等差数列{an}满足d≠0且a2是a1、a4的等比中项,记bn=${a}_{{2}^{n}}$(n∈N*).(Ⅰ)若b2+4是b1+1,b3+3的等差中项,求公差为d的值;
(Ⅱ)当d>0,对任意的正整数n均有$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$<2<$\frac{{a}_{1}+{a}_{3}+…+{a}_{2n-1}}{2n-1}$,求公差d的取值范围.
分析 (Ⅰ)利用a2是a1、a4的等比中项,可得a1=d,an=nd,bn=2nd,根据b2+4是b1+1,b3+3的等差中项,求公差为d的值;
(Ⅱ)利用$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$<2<$\frac{{a}_{1}+{a}_{3}+…+{a}_{2n-1}}{2n-1}$,结合求和公式,即可求公差d的取值范围.
解答 解:(Ⅰ)∵a2是a1、a4的等比中项,
∴(a1+d)2=a1(a1+3d),
∴a1=d,
∴an=nd,∴bn=2nd,
∵b2+4是b1+1,b3+3的等差中项,
∴2(b2+4)=(b1+1)+(b3+3),
∴2(4d+4)=2d+1+8d+3,
∴d=2;
(Ⅱ)$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$=$\frac{1}{d}$($\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$)<2,
∴d>$\frac{1}{2}$(1-$\frac{1}{{2}^{n}}$),
∴d≥$\frac{1}{2}$;
$\frac{{a}_{1}+{a}_{3}+…+{a}_{2n-1}}{2n-1}$=$\frac{1+3+…+2n-1}{2n-1}$d=$\frac{{n}^{2}}{2n-1}$d>2,
∴d>2($\frac{2}{n}$-$\frac{1}{{n}^{2}}$),
∴d>2,
综上,d>2.
点评 本题考查等差数列、等比数列的通项与求和,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.甲、乙两人在一次设计比赛中各射靶5次,两人成绩的条形图如图所示,则( )
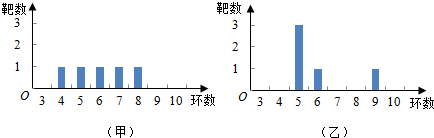

| A. | 甲的成绩的平均数小于乙的成绩的平均数 | |
| B. | 甲的成绩的极差小于乙的成绩的极差 | |
| C. | 甲的成绩的方差小于乙的成绩的方差 | |
| D. | 甲的成绩的中位数等于乙的成绩的中位数 |
