题目内容
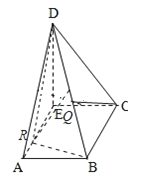
【题目】如图,已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+![]() ,过A作AE⊥CD,垂足为E,现将△ADE沿AE折叠,使得DE⊥EC.
,过A作AE⊥CD,垂足为E,现将△ADE沿AE折叠,使得DE⊥EC.

(1)求证:BC⊥面CDE;
(2)在线段AE上是否存在一点R,使得面BDR⊥面DCB,若存在,求出点R的位置;若不存在,请说明理由.
【答案】(1)略;(2)![]()
【解析】
(1)由已知中![]() ,垂足为
,垂足为![]() ,
,![]() .根据线面垂直的判定定理,我们可得
.根据线面垂直的判定定理,我们可得![]() 面
面![]() .由线面垂直的定义,可得
.由线面垂直的定义,可得![]() ,又由
,又由![]() ,得到
,得到![]() 平面
平面![]() ;(2)取
;(2)取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,求出
,求出![]() ,解
,解![]() ,可得
,可得![]() ,又由等腰
,又由等腰![]() 中,
中,![]() 为底边
为底边![]() 的中点,得到
的中点,得到![]() ,进而根据线面垂直判定定理,及面面垂直判定定理,得到结论.
,进而根据线面垂直判定定理,及面面垂直判定定理,得到结论.
(1)由已知得:![]() ,
,![]() ,
,![]()
![]() 面
面![]() .
.
![]() ,又
,又![]() ,
,![]()
![]() 面
面![]()
(2)分析可知,![]() 点满足
点满足![]() 时,面
时,面![]() 面
面![]() .
.
理由如下:取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
容易计算![]() ,
,
在![]() 中
中
![]()
![]() ,
,
由平行四边形性质得![]() ,
,
所以![]()
可知![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
![]() .
.
又在![]() 中,
中,![]() ,
,![]() 为
为![]() 中点
中点
![]() ,
,
因为![]()
![]() 面
面![]() ,因为
,因为![]() ,
,
![]() 面
面![]() 面
面![]() .
.

【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【题目】某校进行理科、文科数学成绩对比,某次考试后,各随机抽取100名同学的数学考试成绩进行统计,其频率分布表如下.
分组 | 频数 | 频率 | 分组 | 频数 | 频率 | |
[135,150] | 8 | 0.08 | [135,150] | 4 | 0.04 | |
[120,135) | 17 | 0.17 | [120,135) | 18 | 0.18 | |
[105,120) | 40 | 0.4 | [105,120) | 37 | 0.37 | |
[90,105) | 21 | 0.21 | [90,105) | 31 | 0.31 | |
[75,90) | 12 | 0. 12 | [75,90) | 7 | 0.07 | |
[60,75) | 2 | 0.02 | [60,75) | 3 | 0.03 | |
总计 | 100 | 1 | 总计 | 100 | 1 |
理科 文科
(Ⅰ)根据数学成绩的频率分布表,求文科数学成绩的中位数的估计值;(精确到0.01)
(Ⅱ)请填写下面的列联表,并根据列联表判断是否有90%的把握认为数学成绩与文理科有关:
数学成绩 | 数学成绩<120分 | 合计 | |
理科 | |||
文科 | |||
合计 | 200 |
参考公式与临界值表: ![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 | |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】某公司制造两种电子设备:影片播放器和音乐播放器.在每天生产结束后,要对产品进行检测,故障的播放器会被移除进行修复. 下表显示各播放器每天制造的平均数量以及平均故障率.
商品类型 | 播放器每天平均产量 | 播放器每天平均故障率 |
影片播放器 | 3000 | 4% |
音乐播放器 | 9000 | 3% |
下面是关于公司每天生产量的叙述:
①每天生产的播放器有三分之一是影片播放器;
②在任何一批数量为100的影片播放器中,恰好有4个会是故障的;
③如果从每天生产的音乐播放器中随机选取一个进行检测,此产品需要进行修复的概率是0.03.
上面叙述正确的是___________.



