题目内容
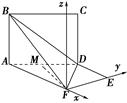
如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,M为AD的中点.
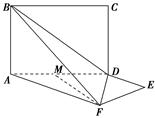
(1)证明:MF⊥BD;
(2)若二面角A-BF-D的平面角的余弦值为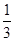 ,求AB的长.
,求AB的长.

(1)证明:MF⊥BD;
(2)若二面角A-BF-D的平面角的余弦值为
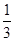 ,求AB的长.
,求AB的长.(1)见解析 (2)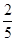
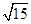
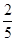
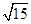
(1)证明 由已知得△ADF为正三角形,所以MF⊥AD,
因为平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD,
MF?平面ADEF,所以MF⊥BD.
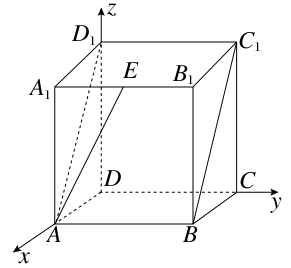
(2)设AB=x,以F为原点,AF,FE所在直线分别为x轴,y轴建立如图所示的空间直角坐标系,则F(0,0,0),A(-2,0,0),D(-1,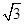 ,0),B(-2,0,x),所以
,0),B(-2,0,x),所以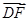 =(1,-
=(1,-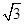 ,0),
,0),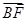 =(2,0,-x).
=(2,0,-x).
因为EF⊥平面ABF,所以平面ABF的法向量可取n1=(0,1,0).
设n2=(x1,y1,z1)为平面BFD的法向量,则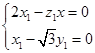
可取n2=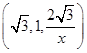 .
.
因为cos〈n1,n2〉=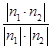 =
=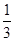 ,
,
得x=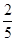
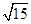 ,所以AB=
,所以AB=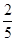
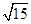 .
.
因为平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD,
MF?平面ADEF,所以MF⊥BD.
(2)设AB=x,以F为原点,AF,FE所在直线分别为x轴,y轴建立如图所示的空间直角坐标系,则F(0,0,0),A(-2,0,0),D(-1,
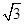 ,0),B(-2,0,x),所以
,0),B(-2,0,x),所以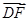 =(1,-
=(1,-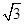 ,0),
,0),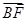 =(2,0,-x).
=(2,0,-x).因为EF⊥平面ABF,所以平面ABF的法向量可取n1=(0,1,0).

设n2=(x1,y1,z1)为平面BFD的法向量,则
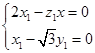
可取n2=
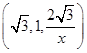 .
.因为cos〈n1,n2〉=
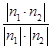 =
=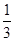 ,
,得x=
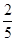
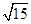 ,所以AB=
,所以AB=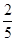
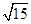 .
.
练习册系列答案
相关题目
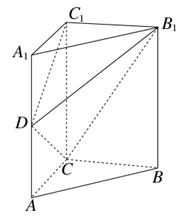
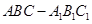 中,
中,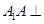 平面
平面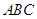 ,
,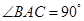 ,
,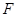 为棱
为棱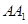 上的动点,
上的动点,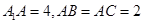 .
.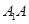 的中点,求直线
的中点,求直线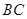 与平面
与平面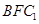 所成角的正弦值;
所成角的正弦值;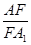 的值为多少时,二面角
的值为多少时,二面角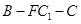 的大小是45
的大小是45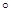 .
.
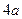 ,将它沿平行于BC的线段PQ折起,使平面APQ⊥平面BPQC,若折叠后AB的长为d,则d的最小值是
,将它沿平行于BC的线段PQ折起,使平面APQ⊥平面BPQC,若折叠后AB的长为d,则d的最小值是
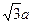
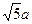
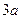
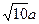
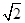
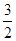 )
)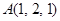 ,
,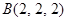 ,点
,点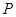 在
在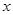 轴上,且
轴上,且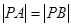 ,则点
,则点