题目内容
【题目】已知![]() ,
,![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() .
.
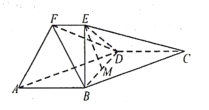
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() ,
,![]() ,连接
,连接![]() 并延长,与轨迹
并延长,与轨迹![]() 交于另一点
交于另一点![]() ,点
,点![]() 是
是![]() 中点,
中点,![]() 是坐标原点,记
是坐标原点,记![]() 与
与![]() 的面积之和为
的面积之和为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)设![]() ,利用
,利用![]() 求得点
求得点![]() 的轨迹
的轨迹![]() 的方程;(2)由
的方程;(2)由![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点,故
的中点,故![]() ,故
,故![]() 与
与![]() 同底等高,故
同底等高,故![]() ,
,![]() ,对斜率分类讨论,联立方程巧用维达表示面积即可.
,对斜率分类讨论,联立方程巧用维达表示面积即可.
试题解析:
(1)设![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
又![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴轨迹![]() 的方程为
的方程为![]() (注:
(注:![]() 或
或![]() ,如不注明扣一分).
,如不注明扣一分).
(2)由![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点,故
的中点,故![]() ,
,
故![]() 与
与![]() 同底等高,故
同底等高,故![]() ,
,![]() ,
,
当直线![]() 的斜率不存在时,其方程为
的斜率不存在时,其方程为![]() ,此时
,此时![]() ;
;
当直线![]() 的斜率存在时,设其方程为:
的斜率存在时,设其方程为:![]() ,设
,设![]() ,
,![]() ,
,
显然直线![]() 不与
不与![]() 轴重合,即
轴重合,即![]() ;
;
联立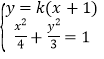 ,解得
,解得![]() ,
,
![]() ,故
,故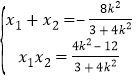 ,
,
故![]()
![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
![]() ,令
,令![]() ,
,
故
![]() ,
,
故![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目