Question

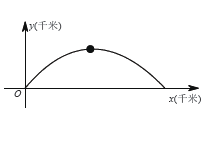
【题目】如图，建立平面直角坐标系， 轴在地平面上， 轴垂直于地平面，单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程表示的曲线上，其中与发射方向有关.炮的射程是指炮弹落地点的横坐标.

（1）求炮的最大射程；

（2）设在第一象限有一飞行物（忽略其大小），其飞行高度为3.2千米，试问它的横坐标不超过多少时，炮弹可以击中它？请说明理由.

Answer 1

【答案】(1) 10千米.(2) 当不超过6千米时，炮弹可以击中目标

【解析】试题分析：（1）求炮的最大射程即求（k＞0）与x轴的横坐标，求出后应用基本不等式求解．（2）求炮弹击中目标时的横坐标的最大值，由一元二次方程根的判别式求解

试题解析：（1）令y＝0，得kx－（1＋k2）x2＝0，

由实际意义和题设条件知x＞0，k＞0，

故x＝＝≤＝10，当且仅当k＝1时取等号．所以炮的最大射程为10千米．

（2）因为a＞0，所以炮弹可击中目标

存在k＞0，使3.2＝ka－（1＋k2）a2成立

关于k的方程a2k2－20ak＋a2＋64＝0有正根

判别式Δ＝（－20a）2－4a2（a2＋64）≥0

a≤6.

所以当a不超过6（千米）时，可击中目标．