题目内容
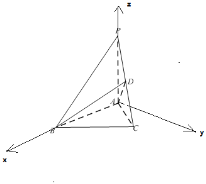
【题目】如图,在底面是正三角形的三棱锥![]() 中,D 为PC的中点,
中,D 为PC的中点,![]() ,
,![]()

(1)求证:![]() 平面
平面![]() ;
;
(2)求 BD 与平面 ABC 所成角的大小;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析(2)![]() (3)
(3)![]()
【解析】
(1)推导出![]() ,
,![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .(2)以
.(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,平面
轴,平面![]() 中垂直于
中垂直于![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系,利用向量法能求出
轴,建立空间直角坐标系,利用向量法能求出![]() 与平面
与平面![]() 所成角.(3)求出平面
所成角.(3)求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,由此能求出二面角
的法向量,由此能求出二面角![]() 的余弦值.
的余弦值.
证明:(1)![]() ,
,![]() ,
,![]() ,
,
![]() 底面是正三角形,
底面是正三角形,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,平面
轴,平面![]() 中垂直于
中垂直于![]() 的直线为
的直线为![]() 轴,
轴,
建立空间直角坐标系,
则![]() ,0,
,0,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,
,![]() ,
,![]() ,0,
,0,![]() ,
,
![]() ,
,![]() .
.
平面![]() 的法向量为
的法向量为![]() ,0,
,0,![]() ,
,
记![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则![]() ,
,
![]()
![]() ,
,
![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
(3)设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,
,
则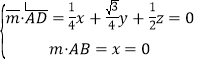 ,取
,取![]() ,得
,得![]() ,2,
,2,![]() .
.
记二面角![]() 的大小为
的大小为![]() ,
,
则![]() ,
,
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】《中华人民共和国个人所得税法》第十四条中有下表(部分):
个人所得税税率(工资、薪金所得适用)
级数 | 全月应纳所得额 | 税率(%) |
1 | 不超过 |
|
2 | 超过 |
|
3 | 超过 |
|
4 | 超过 |
|
5 | 超过 |
|
上表中“全月应纳税所得额”是从月工资、薪金收入中减去![]() 元后的余额.如果某人月工资、薪金收入为
元后的余额.如果某人月工资、薪金收入为![]() 元,那么他应纳的个人所得税为________元.
元,那么他应纳的个人所得税为________元.