题目内容
椭圆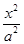 +
+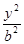 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是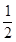 ,则
,则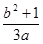 的最小值为( )
的最小值为( )
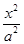 +
+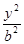 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是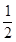 ,则
,则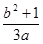 的最小值为( )
的最小值为( )A.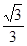 | B.1 | C.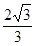 | D.2 |
A
试题分析:因为椭圆
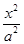 +
+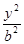 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是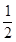 ,所以
,所以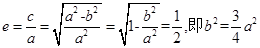 ,
,所以
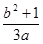
 ,所以
,所以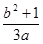 的最小值为
的最小值为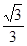 。
。点评:直接考查椭圆的离心率和基本不等式的综合应用。注意基本不等式应用的条件:一正二定三相等。

练习册系列答案
相关题目
题目内容
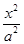 +
+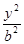 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是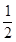 ,则
,则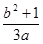 的最小值为( )
的最小值为( )A.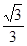 | B.1 | C.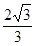 | D.2 |
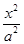 +
+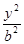 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是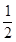 ,所以
,所以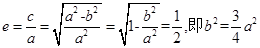 ,
,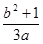
 ,所以
,所以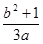 的最小值为
的最小值为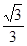 。
。