题目内容
正三棱锥的侧面与底面所成的角的余弦值为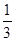 ,则侧棱与底面所成角的正弦值为( )
,则侧棱与底面所成角的正弦值为( )
A.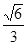 | B.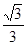 | C.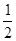 | D.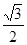 |
A
解析试题分析:设正三棱锥的底面边长为a,侧棱长为b,设底面中心为O,BC的中点为E,连接OE,AE,OC,则 为正三棱锥的侧面与底面所成的角,
为正三棱锥的侧面与底面所成的角, 为侧棱与底面所成的角。易知:AE=
为侧棱与底面所成的角。易知:AE=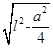 ,所以
,所以 ,所以AO=
,所以AO=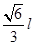 ,设侧棱与底面所成角为
,设侧棱与底面所成角为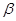 ,则
,则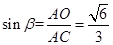 .
.
考点:二面角;线面角;正三棱锥的结构特征。
点评:此题的关键是找出底面边长和侧棱长之间的关系。属于中档题。

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
设 为两条直线,
为两条直线, 为两个平面,下列四个命题中,正确的命题是( )
为两个平面,下列四个命题中,正确的命题是( )
A.若 与 与 所成的角相等,则 所成的角相等,则 |
B.若 , , , , ,则 ,则 |
C.若 , , , , ,则 ,则 |
D.若 , , , , ,则 ,则 |
在三棱柱 中,各棱长相等,侧掕垂直于底面,点
中,各棱长相等,侧掕垂直于底面,点 是侧面
是侧面 的中心,则
的中心,则 与平面
与平面 所成角的大小是 ( )
所成角的大小是 ( )
A.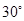 | B.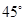 | C. | D. |
设 、b是两条不同的直线,
、b是两条不同的直线, 、
、 是两个不同的平面,则下列四个命题中正确的是( )
是两个不同的平面,则下列四个命题中正确的是( )
A.若 ⊥b, ⊥b, ⊥ ⊥ ,则b∥ ,则b∥ | B.若 ∥ ∥ , , ⊥ ⊥ ,则 ,则 ⊥ ⊥ |
C.若 ⊥ ⊥ , , ⊥ ⊥ ,则 ,则  ∥ ∥ | D.若 ⊥b, ⊥b, ⊥ ⊥ ,b⊥ ,b⊥ ,则 ,则 ⊥ ⊥ |
正方体 中,直线
中,直线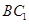 与
与 ( )
( )
| A.异面且垂直 | B.异面但不垂直 |
| C.相交且垂直 | D.相交但不垂直 |
在正三棱锥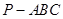 中,
中,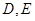 分别是
分别是 的中点,有下列三个论断:
的中点,有下列三个论断:
①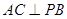 ;②
;②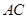 //平面
//平面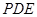 ;③
;③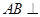 平面
平面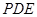 ,
,
其中正确论断的个数为 ( )
| A.3个 | B.2个 | C.1个 | D.0个 |
球内接正四棱锥的高为3,体积为6,则这个球的表面积是( )
| A.16π | B.20π | C.24π | D.32π |
已知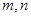 是两条不同直线,
是两条不同直线,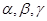 是三个不同平面,下列命题正确的( )
是三个不同平面,下列命题正确的( )
A.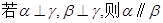 | B.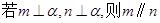 | C.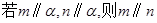 | D.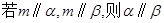 |
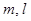 ,平面
,平面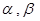 ,且
,且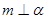 ,
,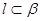 ,给出下列命题
,给出下列命题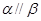 ,则
,则 (2)若
(2)若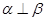 ,则
,则