题目内容
在正三棱锥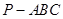 中,
中,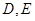 分别是
分别是 的中点,有下列三个论断:
的中点,有下列三个论断:
①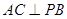 ;②
;②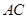 //平面
//平面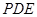 ;③
;③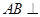 平面
平面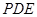 ,
,
其中正确论断的个数为 ( )
| A.3个 | B.2个 | C.1个 | D.0个 |
C
解析试题分析:根据正三棱锥的性质及三垂线定理知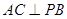 ,故命题①正确;∵
,故命题①正确;∵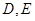 分别是
分别是 的中点,∴AC与面
的中点,∴AC与面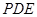 相交于点E,故命题②错误;对于命题③,假设
相交于点E,故命题②错误;对于命题③,假设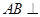 平面
平面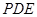 ,则有
,则有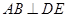 ,显然错误,故正确命题个数为1个,选C
,显然错误,故正确命题个数为1个,选C
考点:本题考查了正三棱锥的性质及线面关系的判断
点评:弄清正棱锥中线面关系及线面平行、垂直定理是解决此类问题的关键

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
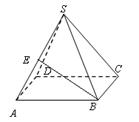
如图,在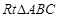 中,
中,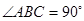 ,
,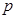 为△ABC所在平面外一点,PA⊥面ABC,则四面体P-ABC中共有直角三角形个数为
为△ABC所在平面外一点,PA⊥面ABC,则四面体P-ABC中共有直角三角形个数为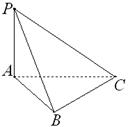
| A.4 | B.3 | C.2 | D.1 |
正三棱锥的侧面与底面所成的角的余弦值为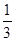 ,则侧棱与底面所成角的正弦值为( )
,则侧棱与底面所成角的正弦值为( )
A.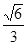 | B.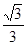 | C.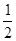 | D.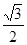 |
如果对于空间任意n(n≥2)条直线总存在一个平面α,使得这n条直线与平面α所成的角均相等,那么这样的n( )
| A.最大值为3 | B.最大值为4 | C.最大值为5 | D.不存在最大值 |
设m、n是两条不同的直线,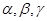 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若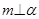 ,
,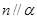 ,则
,则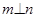 ②若
②若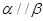 ,
,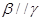 ,
,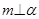 ,则
,则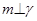
③若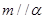 ,
,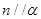 ,则
,则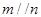 ④若
④若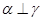 ,
, 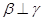 ,则
,则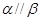
其中正确命题的序号是 ( )
| A.①② | B.②③ | C.③④ | D.①②③④ |
在正方体ABCD-A1B1C1D1中与AD1成600角的面对角线的条数是( )
| A.4条 | B.6条 | C.8条 | D.10条 |
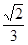
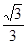
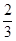
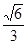
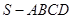 的底面边长为2,高为2,
的底面边长为2,高为2,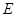 为边
为边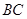 的中点,动点
的中点,动点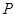 在表面上运动,并且总保持
在表面上运动,并且总保持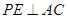 ,则动点
,则动点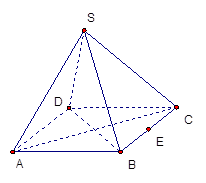
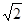
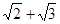
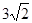
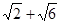
 侧棱长为
侧棱长为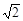 ,底面边长为
,底面边长为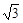 ,
, 是
是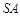 的中点,则异面直线
的中点,则异面直线 与
与 所成角的大小为( )
所成角的大小为( )