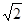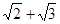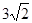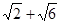题目内容
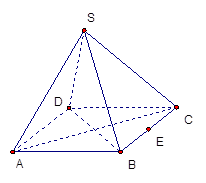
在三棱柱 中,各棱长相等,侧掕垂直于底面,点
中,各棱长相等,侧掕垂直于底面,点 是侧面
是侧面 的中心,则
的中心,则 与平面
与平面 所成角的大小是 ( )
所成角的大小是 ( )
A.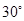 | B.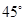 | C. | D. |
C
解析试题分析:根据已知条件,由于在三棱柱 中,各棱长相等,侧掕垂直于底面,点
中,各棱长相等,侧掕垂直于底面,点 是侧面
是侧面 的中心,那么取BC的中点E,那么连接AE,故AE垂直平面
的中心,那么取BC的中点E,那么连接AE,故AE垂直平面 ,那么可知角ADE即为所求的线面的大小,设边长为2,那么ED=1,AD=2,则根据直角三角形的边角关系可知,线面角的大小为
,那么可知角ADE即为所求的线面的大小,设边长为2,那么ED=1,AD=2,则根据直角三角形的边角关系可知,线面角的大小为 ,故选C.
,故选C.
考点:本试题考查线面角。
点评:解决该试题的关键是利用线面角的定义,找到平面的垂线,然后得到斜线在平面内的射影,进而得到线面角,属于基础题。

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
如图,平行六面体 中,侧棱
中,侧棱 长为3,底面是边长为2的菱形,
长为3,底面是边长为2的菱形,
 点E在棱
点E在棱 上,则
上,则 的最小值为( )
的最小值为( )
A. | B.5 | C. | D.7 |
已知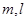 是两条不同的直线,
是两条不同的直线,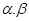 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题:
①若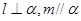 ,则
,则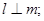 ②若
②若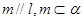 则
则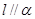 ;
;
③若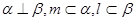 则
则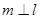 ; ④若
; ④若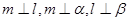 则
则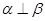 ;
;
其中正确命题的个数为 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
正方体 中,下列结论错误的是
中,下列结论错误的是
A. ∥平面 ∥平面 | B. 平面 平面 |
C. | D.异面直线 与 与 所成的角是45º 所成的角是45º |
正方体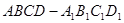 中,
中, 与平面
与平面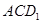 所成的角的余弦值为( )
所成的角的余弦值为( )
A.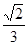 | B.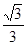 | C. | D.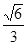 |
正三棱锥的侧面与底面所成的角的余弦值为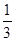 ,则侧棱与底面所成角的正弦值为( )
,则侧棱与底面所成角的正弦值为( )
A.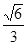 | B.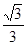 | C.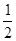 | D.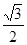 |
a、b、c为三条不重合的直线,α、β、γ为三个不重合的平面,现给出六个命题: 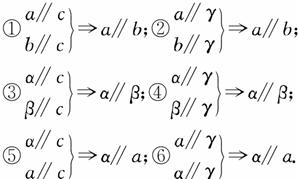
其中正确的命题是( )
| A.①②③ | B.①④⑤ | C.①④ | D.①④⑤⑥ |
 一边BC在平面
一边BC在平面 内,顶点A在平面
内,顶点A在平面 ,三角形所在平面与
,三角形所在平面与 ,则直线
,则直线 与
与

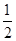

 的底面边长为2,高为2,
的底面边长为2,高为2, 为边
为边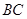 的中点,动点
的中点,动点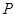 在表面上运动,并且总保持
在表面上运动,并且总保持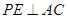 ,则动点
,则动点