题目内容
17.作出下列函数的图象,并指出其值域.(1)y=x2+x(-1≤x≤1);
(2)y=$\frac{2}{x}$(-2≤x≤1,且x≠0).
分析 (1)画出函数的图象,然后求出函数的值域;
(2)画出函数的图象,然后求出函数的注意;
解答 解:(1)y=x2+x(-1≤x≤1);函数的图象为: ,
,
函数的值域为:[-$\frac{1}{4}$,2]
(2)y=$\frac{2}{x}$(-2≤x≤1,且x≠0).函数的图象为: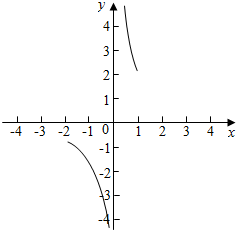
函数的值域为:(-∞,-1]∪[2,+∞).
点评 本题考查函数的图象的画法,函数的值域的求法,考查计算能力以及作图能力.

练习册系列答案
相关题目
7.在△ABC中,a,b,c分别是角A,B,C的对边,若a,b,c成等比数列,A=60°,则$\frac{bsinB}{c}$=( )
| A. | $\frac{3}{4}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |