题目内容
5.在极坐标系中,作出下列各点:(1)A(2,$\frac{π}{6}$),B(6,-120°),C(1,$\frac{π}{3}$),
D(4,-$\frac{3π}{4}$),E(4,0),F(2.5,180°);
(2)A(3,$\frac{π}{3}$),B(3,$\frac{π}{6}$),C(3,$\frac{π}{2}$),D(3,π),E(3,$\frac{3π}{2}$),并说明这5个点有什么关系;
(3)A(-2,$\frac{π}{6}$),B(-1,$\frac{π}{6}$),C(3,$\frac{π}{6}$),D(4.5,$\frac{π}{6}$),E(4.55,$\frac{π}{6}$),并说明这5个点有什么关系.
分析 由条件利用极坐标的定义画出各点在极坐标系中的位置,从而得出结论.
解答 解:(1)如图(1)所示: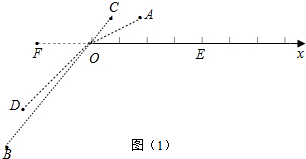
(2)A、B、C、D、E这5个点都在以极点为圆心、半径等于3的圆上,
如图(2)所示: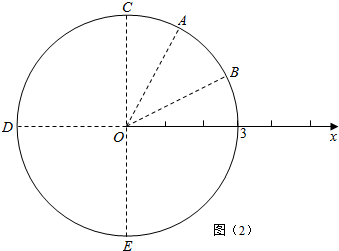
(3)A、B、C、D、E这5个点都在直线θ=$\frac{π}{6}$上,如图(3)所示: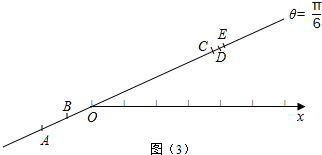
点评 本题主要考查用极坐标刻画点在极坐标系中的位置,属于基础题.

练习册系列答案
相关题目
16.根据下面某工程的工作明细表:
(1)画出工作流程图;
(2)指出关键路径;
(3)确定完成工程的最短总工期.
| 工作代码 | 紧前工作 | 工期(天) |
| A | 无 | 7 |
| B | 无 | 3 |
| C | 无 | 1 |
| D | C | 3 |
| E | A,B,D | 3 |
| F | E | 2 |
| G | A,B,D | 2 |
| H | F,G | 1 |
(2)指出关键路径;
(3)确定完成工程的最短总工期.
15.下列函数中,在区间(-1,1)上为增函数的是( )
| A. | y=x-x2 | B. | y=|x+1| | C. | y=-$\frac{1}{x}$ | D. | y=x2-2x |