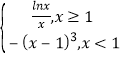题目内容
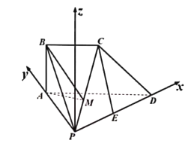
【题目】如图,在四棱锥![]() 中,平面ABCD平面PAD,
中,平面ABCD平面PAD,![]() ,
,![]() ,
,![]() ,
,![]() ,E是PD的中点.
,E是PD的中点.

![]() 证明:
证明:![]() ;
;
![]() 设
设![]() ,点M在线段PC上且异面直线BM与CE所成角的余弦值为
,点M在线段PC上且异面直线BM与CE所成角的余弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)由平面![]() 平面
平面![]() 的性质定理得
的性质定理得![]() 平面
平面![]() ,
,![]() .在
.在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,![]() 平面
平面![]() ,即可得
,即可得![]() ;
;
(2)以![]() 为坐标原点建立空间直角坐标系,由空间向量法和异面直线
为坐标原点建立空间直角坐标系,由空间向量法和异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,得点M的坐标,从而求出二面角
,得点M的坐标,从而求出二面角![]() 的余弦值.
的余弦值.
(1)![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() =
=![]() ,
,![]() ,所以
,所以![]() .由面面垂直的性质定理得
.由面面垂直的性质定理得![]() 平面
平面![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() 由正弦定理可得:
由正弦定理可得:![]() ,
,
![]() ,即
,即![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
(2)以![]() 为坐标原点建立如图所示的空间直角坐标系,则
为坐标原点建立如图所示的空间直角坐标系,则![]() ,
,![]() ,
,
![]() ,设
,设![]()
![]() ,则
,则![]() ,
,
![]() ,
,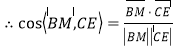
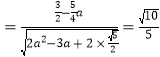
得![]() ,
,![]() ,而
,而![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,由
,由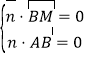 可得:
可得:![]() ,令
,令![]() ,则
,则![]() ,取平面
,取平面![]() 的法向量
的法向量![]() ,则
,则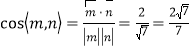 ,故二面角
,故二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
女 | 18 | ||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
【题目】某城市的公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,经过调查得出了如下数据:
之间的关系,经过调查得出了如下数据:
间隔时间( | 10 | 11 | 12 | 13 | 14 | 15 |
等待人数( | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这六组数据中选取四组数据作线性回归分析,然后用剩下的两组数据进行检验
(1)求从这六组数据中选取四组数据后,剩下的的两组数据不相邻的概率:
(2)若先取的是后面四组数据,求![]() 关干
关干![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)规定根据(2)中线性回归方程预利的数据与用剩下的两组实际数据相差不超过![]() 人,则所求出的线性回归方程是“最佳回归方程”,请判断(2)中所求的是 “最佳回归方程”吗?为了使等候的乘客不超过
人,则所求出的线性回归方程是“最佳回归方程”,请判断(2)中所求的是 “最佳回归方程”吗?为了使等候的乘客不超过![]() 人,则间隔时间设置为
人,则间隔时间设置为![]() 分钟合适吗?
分钟合适吗?
附:对于一组组数据![]() , 其回归直线
, 其回归直线![]() +的斜率和截距的最小二乘估计分别为:
+的斜率和截距的最小二乘估计分别为:  ,
,![]()